Bài 2.53 trang 56 SGK Toán lớp 6 tập 1 - KNTT
Câu hỏi:
Tìm x ∈ {50; 108; 189; 1 234; 2 019; 2 020} sao cho:
a) x - 12 chia hết cho 2;
b) x - 27 chia hết cho 3;
c) x + 20 chia hết cho 5;
d) x + 36 chia hết cho 9.
Phương pháp:
* Các số có chữ số tận cùng là 0;2;4;6 hoặc 8 thì chia hết cho 2
* Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5
* Các số có tổng các chữ số là một số chia hết cho 3 thì chia hết cho 3
* Các số có tổng các chữ số là một số chia hết cho 9 thì chia hết cho 9
Lời giải:
a) x - 12 chia hết cho 2
Vì 12 chia hết cho 2 nên x chia hết cho 2 do đó x tận cùng là số chẵn
Mà x ∈ {50; 108; 189; 1 234; 2 019; 2 020}
Vậy giá trị của x thỏa mãn là 50, 108, 1 234, 2 020.
b) x - 27 chia hết cho 3;
Vì 27 chia hết cho 3 nên x chia hết cho 3 do đó tổng các chữ số của x chia hết cho 3
Mà x ∈ {50; 108; 189; 1 234; 2 019; 2 020}

Vậy giá trị của x thỏa mãn là 108, 189, 2 019.
c) x + 20 chia hết cho 5;
Vì 20 chia hết cho 5 nên x chia hết cho 5 do đó x có chữ số tận cùng là 0 hoặc 5
Mà x ∈ {50; 108; 189; 1 234; 2 019; 2 020}
Vậy giá trị của x thỏa mãn là 50, 2 020.
d) x + 36 chia hết cho 9
Vì 36 chia hết cho 9 nên x chia hết cho 9 do đó tổng các chữ số của x chia hết cho 9
Mà x ∈ {50; 108; 189; 1 234; 2 019; 2 020}
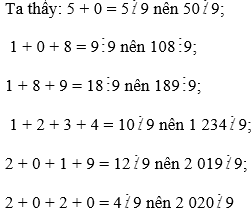
Vậy giá trị của x thỏa mãn là 108, 189.
Bài 2.54 trang 56 SGK Toán lớp 6 tập 1 - KNTT
Câu hỏi:
Thực hiện phép tính sau rồi phân tích kết quả ra thừa số nguyên tố:
a) 142 + 52 + 22;
b) 400 : 5 + 40
Phương pháp:
- Thực hiện phép tính theo thứ tự: Lũy thừa => Nhân, chia => Cộng, trừ.
- Phân tích kết quả ra thừa số nguyên tố.
Lời giải:
a) 142 + 52 + 22 = 196 + 25 + 4 = 225
Phân tích 225 ra thừa số nguyên tố:

Vậy 142 + 52 + 22 = 225 = 32.52
b) 400 : 5 + 40 = 80 + 40 = 120
Phân tích 120 ra thừa số nguyên tố
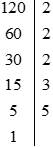
Vậy 400 : 5 + 40 = 120 = 23.3.5.
Bài 2.55 trang 56 SGK Toán lớp 6 tập 1 - KNTT
Câu hỏi:
Tìm ƯCLN và BCNN của:
a) 21 và 98;
b) 36 và 54.
Phương pháp:
- Phân tích mỗi số ra thừa số nguyên tố,
- Chọn ra các thừa số nguyên tố chung và riêng;
- Lập tích các thừa số đã chọn, mỗi thùa Số lấy với số mũ lớn nhất, Tích đó là BCNN
cần tìm.
- Phân tích mỗi số ra thừa số nguyên tố,
- Chọn ra các thừa số nguyên tố chung và riêng;
- Lập tích các thừa số đã chọn, mỗi thùa Số lấy với số mũ lớn nhất, Tích đó là BCNN cần tìm.
Lời giải:
a) Ta có: 21 = 3.7; 98 = 2.72
+) Thừa số nguyên tố chung là 7, thừa số nguyên tố riêng là 2 và 3
+) Số mũ nhỏ nhất của 7 là 1 nên ƯCLN(21, 98) = 7
+) Số mũ lớn nhất của 2 là 1, số mũ lớn nhất của 3 là 1, số mũ lớn nhất của 7 là 2 nên BCNN(21, 98) = 2.3.72= 294
Vậy ƯCLN(21, 98) = 7 ; BCNN(21, 98) = 2.3.72= 294.
b) Ta có: 36 = 22.32; 54 = 2.33
+) Thừa số nguyên tố chung là 2 và 3, không có thừa số nguyên tố riêng
+) Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 3 là 2 nên ƯCLN(36, 54) = 2.32 = 18
+) Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 3 nên BCNN(36, 54) = 2.32 = 108
Vậy ƯCLN(36, 54) = 2.32 = 18; BCNN(36, 54) = 2.32 = 108.
Bài 2.56 trang 56 SGK Toán lớp 6 tập 1 - KNTT
Câu hỏi:
Các phân số sau đã tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản.
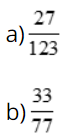
Phương pháp:
Nếu ƯCLN của tử và mẫu bằng 1 thì phân số đã cho tối giản.
Nếu ƯCLN của tử và mẫu lớn hơn 1 thì phân số chưa tối giản. Khi đó ta đi chia cả tử và mẫu cho ƯCLN thì được
phân số tối giản.
Lời giải:
a) Ta có: 27 = 33; 123 = 3.41
+) Thừa số nguyên tố chung là 3
+) Số mũ nhỏ nhất của 3 là 1 nên ƯCLN(27, 123) = 3. Do đó phân số  chưa tối giản.
chưa tối giản.
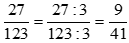 . Ta được
. Ta được  là phân số tối giản vì ƯCLN(9, 41) = 1.
là phân số tối giản vì ƯCLN(9, 41) = 1.
b) Ta có: 33 = 3.11; 77 = 7.11
+) Thừa số nguyên tố chung là 11
+) Số mũ nhỏ nhất của 11 là 1 nên ƯCLN(33, 77) = 11. Do đó phân số  chưa tối giản.
chưa tối giản.
 . Ta được
. Ta được  là phân số tối giản vì ƯCLN(3, 7) = 1.
là phân số tối giản vì ƯCLN(3, 7) = 1.
Bài 2.57 trang 56 SGK Toán lớp 6 tập 1 - KNTT
Câu hỏi:
Thực hiện phép tính: 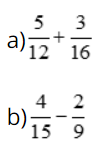
Phương pháp:
Quy đồng mẫu số các phân số rồi thực hiện cộng(trừ) tử số các phân số và giữ nguyên mẫu số.
Lời giải:
a) Ta có: 12 = 22.3; 16 = 24 nên BCNN(12, 16) = 24.3 = 48 nên ta có thể chọn mẫu chung là 48.
b) Ta có: 15 = 3.5; 9 = 32 nên BCNN(15, 9) = 32.5 = 45 nên ta có thể chọn mẫu chung là 45.
Bài 2.58 trang 56 SGK Toán lớp 6 tập 1 - KNTT
Câu hỏi:
Có 12 quả cam, 18 quả xoài và 30 quả bơ. Mẹ muốn Mai chia đều mỗi loại quà đó vào các túi quà sao cho mỗi túi đều có cả cam, xoài và bơ. Hỏi Mai có thể chia được nhiều nhất là mấy túi quả?
Phương pháp:
Số túi quà nhiều nhất mà Mai có thể chia được là ƯCLN(12, 18, 30).
Lời giải:
Số túi quà nhiều nhất mà Mai chia được là ƯCLN(12, 18, 30)
Ta có: 12 = 22.3
18 = 2.32
30 = 2.3.5
+) Các thừa số nguyên tố chung là 2 và 3. Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 4 là 1
Do đó: ƯCLN(12, 18, 30) = 2.3 = 6
Vậy Mai có thể chia được nhiều nhất 6 túi quà.
Bài 2.59 trang 56 SGK Toán lớp 6 tập 1 - KNTT
Câu hỏi:
Bác Nam định kì 3 tháng một lần thay dầu, 6 tháng một lần xoay lốp xe ô tô của mình. Hỏi nếu bác ấy làm hai việc đó cùng lúc vào tháng 4 năm nay, thì lần gần nhất tiếp theo bác ấy sẽ cùng làm hai việc đó vào tháng nào?
Phương pháp:
Số tháng ít nhất tiếp theo mà bác Nam làm hai việc đó cùng một tháng là BCNN(3, 6).
Lời giải:
Số tháng ít nhất tiếp theo mà bác Nam làm hai việc đó cùng một tháng là BCNN(3, 6)
Vì 6\( \vdots \)3 nên BCNN(3, 6) = 6
Do đó sau 6 tháng nữa bác sẽ làm hai việc cùng một tháng.
Nếu bác ấy làm hai việc đó cùng lúc vào tháng 4 năm nay, thì gần nhất lần tiếp theo bác ấy sẽ cùng làm hai việc đó vào tháng 4 + 6 = 10.
Vậy lần gần nhất tiếp theo bác ấy sẽ cùng làm hai việc đó vào tháng 10.
Bài 2.60 trang 56 SGK Toán lớp 6 tập 1 - KNTT
Câu hỏi:
Biết rằng 79 và 97 là hai số nguyên tố. Hãy tìm ƯCLN và BCNN của hai số này.
Phương pháp:
Nếu a và b là hai số nguyên tố cùng nhau thì:
ƯCLN(a, b) = 1 và BCNN(a, b) = a.b.
Lời giải:
Vì mỗi số nguyên tố chỉ có ước là 1 và chính nó mà 79 và 97 là hai số nguyên tố khác nhau nên ƯCLN(79, 97) = 1 và BCNN(79, 97) = 79.97 = 7 663.
Bài 2.61 trang 56 SGK Toán lớp 6 tập 1 - KNTT
Câu hỏi:
Biết hai số 3a. 52 và 33.5b có ƯCLN là 33.52 và BCNN là 34 .53. Tìm a và b.
Phương pháp:
Tích hai số m và n bằng tích của ƯCLN(m, n) và BCNN(m, n)
Lời giải:
ƯCLN (3a.52; 33.5b). BCNN = (3a.52; 33.5b) = ( 33.53).(34.53)
= (33.34).(52.53) = 33+4.52+3 = 37.55
Tích của 2 số đã cho:(3a.52).(33.5b) = ( 3a.33).(52.5b) = 3a+3.5b+2
Ta có tích của hai số bằng tích của ƯCLN và BCNN của hai số ấy nên:
37.55= 3a+3.5b+2. Do đó: a + 3 = 7 ⇒ a = 7 – 3 = 4
và b + 2 = 5 ⇒ b = 5 -2
Vậy a = 4 và b = 3.
Bài 2.62 trang 56 SGK Toán lớp 6 tập 1 - KNTT
Câu hỏi:
Bác kia chăn vịt khác thường
Buộc đi cho được chẵn hàng mới ra
Hàng 2 xếp thấy chưa vừa
Hàng 3 xếp vẫn còn thừa một con
Hàng 4 xếp vẫn chưa tròn
Hàng 5 xếp thiếu một con mới đầy
Xếp thành hàng 7, đẹp thay
Vịt bao nhiêu? Tính được ngay mới tài.
(Biết số vịt chưa đến 200 con).
Phương pháp:
Áp dụng các dấu hiệu chia hết cho 2, 3,4,7 để tìm được số vịt
Lời giải:
Giả sử có a con vịt.
Theo các dữ kiện đề bài cho:
Hàng 2 xếp vẫn chưa vừa nghĩa là a là số lẻ ⇒ a + 1 ⋮ 2 (1)
Hàng 3 xếp vẫn còn thừa 1 con nghĩa là (a – 1) ⋮ 3 (2)
Hàng xếp 5 thiếu 1 con mới đầy nghĩa là (a + 1) ⋮ 5 (3)
Xếp thành hàng 7, đẹp thay nghĩa là a ⋮ 7 (4)
Số vịt chưa đến 200 con nghĩa là a < 200.
Từ (1) và (3) suy ra (a + 1) ∈ BC(2; 5) = B(10) = {0; 10; 20; 30; 40; …}.
a ⋮ 7 nên a + 1 chia 7 dư 1.
Các số là bội của 10, chia 7 dư 1 là 50; 120; 190; 260; …
Mà a + 1 ≤ 200 nên a + 1 = 50; 120 hoặc 190.
– Trường hợp 1: a + 1 = 50 thì a = 49 ⋮ 7 (t/m (4))
a – 1 = 48 ⋮ 3 (t/m (2)).
Vậy a = 49 (thỏa mãn).
– Trường hợp 2: a + 1= 120
Suy ra a = 119, suy ra a – 1 = 118 ⋮̸ 3 (không thỏa mãn (2)) (Loại).
– Trường hợp 3: a + 1 = 190
Suy ra a = 189, suy ra a – 1 = 188 ⋮̸ 3 (không thỏa mãn (2)) (Loại).
Vậy số vịt là 49 con.
Giaibaitap.me
Giải bài tập 3.1; 3.2; 3.3; 3.4; 3.5; 3.6; 3.7; 3.8 trang 61 sách giáo khoa Toán lớp 6 Kết nối tri thức với cuộc sống tập 1 - Bài 13 Tập hợp các số nguyên
Giải bài tập 3.9; 3.10; 3.11; 3.12; 3.13; 3.14; 3.15; 3.16; 3.17; 3.18 trang 66 sách giáo khoa Toán lớp 6 Kết nối tri thức với cuộc sống tập 1 - Bài 14 Phép cộng và phép trừ số.
Giải bài tập 3.19; 3.20; 3.21; 3.22; 3.23 trang 68 sách giáo khoa Toán lớp 6 Kết nối tri thức với cuộc sống tập 1 - Bài 15 Quy tắc dấu ngoặc.
Giải bài tập 3.24; 3.25; 3.26; 3.27; 3.28; 3.29; 3.30; 3.31 trang 69 sách giáo khoa Toán lớp 6 Kết nối tri thức với cuộc sống tập 1 - Bài Luyện tập chung
