Bài 2.30 trang 48 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi: 

Tìm tập hợp ước chung của:

a) 30 và 45            b) 42 và 70.

Phương pháp: 

- Tìm tập hợp các ước của các số đã cho.

- Lấy các số chung trong các tập hợp vừa tìm được.

Lời giải: 

a) Phân tích các số 30 và 45 ra thừa số nguyên tố:

30 = 2.3.5;           45 = 3².5

+) Ta chọn ra các thừa số nguyên tố chung là: 3 và 5.

+) Số mũ nhỏ nhất của 3 là 1, số mũ nhỏ nhất của 5 là 1. Khi đó:

 ƯCLN(30, 45) = 3.5 = 15. Ta được ƯC(30; 45) = Ư(15) = {1; 3; 5; 15}

Vậy ƯC(30; 45) = {1; 3; 5; 15}.

b) Phân tích các số 42 và 70 ra thừa số nguyên tố:

42 = 2.3.7;           70 = 2.5.7;

+) Ta chọn ra các thừa số nguyên tố chung là: 2 và 7.

+) Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 7 là 1. Khi đó:

 ƯCLN(42, 70) = 2.7 = 14. Ta được ƯC(42; 70) = Ư(14) = {1; 2; 7; 14}

Vậy ƯC(42; 70) = {1; 2; 7; 14}.

Bài 2.31 trang 48 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi:

Tìm ƯCLN của hai số:

a) 40 và 70;           b) 55 và 77.

Phương pháp: 

Các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1:

- Phân tích mỗi số ra thừa số nguyên tố

- Chọn ra các thừa số nguyên tố chung;

- Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.

Lời giải: 

a) Phân tích các số 40 và 70 ra thừa số nguyên tố ta được:

40 = 2³.5;                             70 = 2.5.7

Ta thấy 2 và 5 là các thừa số nguyên tố chung của 40 và 70. Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 5 là 1 nên ƯCLN(40, 70) = 2. 5 = 10

Vậy ƯCLN(40, 70) = 10.

b) Phân tích các số 55 và 77 ra thừa số nguyên tố ta được:

55 = 5. 11;                              77 = 7. 11                          

Ta thấy 11 thừa số nguyên tố chung của 55 và 77. Số mũ nhỏ nhất của 11 là 1 nên ƯCLN(55, 77) = 11

Vậy ƯCLN(40, 70) = 11.

Bài 2.32 trang 48 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi: 

Tìm ƯCLN của:

a) 2². 5 và 2. 3. 5

b)  \(2^4. 3;  2^2.3^2. 5\) và \(2^4.11.\)

Phương pháp:

- Chọn ra các thừa số nguyên tố chung;

- Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.

Lời giải: 

a) Phân tích các số 40 và 70 ra thừa số nguyên tố ta được:

40 = 2³.5;                             70 = 2.5.7

Ta thấy 2 và 5 là các thừa số nguyên tố chung của 40 và 70. Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 5 là 1 nên ƯCLN(40, 70) = 2. 5 = 10

Vậy ƯCLN(40, 70) = 10.

b) Phân tích các số 55 và 77 ra thừa số nguyên tố ta được:

55 = 5. 11;                              77 = 7. 11                          

Ta thấy 11 thừa số nguyên tố chung của 55 và 77. Số mũ nhỏ nhất của 11 là 1 nên ƯCLN(55, 77) = 11

Vậy ƯCLN(40, 70) = 11.

Bài 2.33 trang 48 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi: 

Cho hai số a = 72 và b = 96.

a) Phân tích a và b ra thừa số nguyên tố;

b) Tìm ƯCLN(a, b), rồi tìm ƯC(a, b).

Phương pháp: 

a) Phân tích mỗi số ra thừa số nguyên tố

b)  Chọn ra các thừa số nguyên tố chung;

     Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.

=> Ước chung của một số là ước của ước chung lớn nhất của số đó

Lời giải:

a) Phân tích a và b ra thừa số nguyên tố

Ta có:

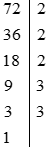
 Do đó: a = 72 = 23.32.

Lại có:

 Vậy  b = 96 = 25.3.

b) Ta thấy 2 và 3 là các thừa số chung của 70 và 96. Số mũ nhỏ nhất của 2 là 3 và số mũ nhỏ nhất của 3 là 1 nên

ƯCLN(72; 96) = 23 . 3 = 24

ƯC(a, b) = Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}.

Bài 2.34 trang 48 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi:

Các phân số sau đã là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản?

Phương pháp:

Nếu tử và mẫu của phân số đã cho có ước chung lớn nhất khác 1 thì phân số chưa tối giản, nếu có ước chung lớn nhất bằng 1 thì phân số đã tối giản.

Lời giải: 

a) Ta có:

50 = 2.52;           85 = 5.17

+) Thừa số nguyên tố chung là 5 với số mũ nhỏ nhất là 1 nên ƯCLN(50, 85) = 5.  

Do đó 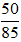 không là phân số tối giản.

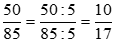 . Ta được  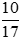là phân số tối giản vì ƯCLN(10, 17) = 1.

b) Ta có:

23 = 23;           81 = 34

Nên 23 và 81 không có thừa số nguyên tố chung nên ƯCLN(23, 81) = 1.  

Do đó 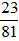 là phân số tối giản.

Bài 2.35 trang 48 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi: 

Hãy cho hai ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số.

Phương pháp:

Tìm các số có ƯCLN bằng 1 mà cả hai đều là hợp số.

Lời giải: 

Có nhiều ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số, chẳng hạn ta có hai ví dụ sau:

+) 6 và 35

Vì 6 = 2.3; 35 = 5.7. Hai số này không có thừa số nguyên tố chung nên ƯCLN bằng 1 nhưng 6 chia hết cho 2 nên 6 là hợp số; 35 chia hết cho 5 nên 35 là hợp số.

+) 10 và 27

Vì 10 = 2.5; 27 = 33. Hai số này không có thừa số nguyên tố chung nên ƯCLN bằng 1 nhưng 10 chia hết cho 2 nên 10 là hợp số; 27 chia hết cho 3 nên 27 là hợp số.

 Giaibaitap.me