Bài 1 trang 24 SGK Toán lớp 6 tập 1 - Cánh Diều

Câu hỏi:

Viết các tích sau dưới dạng lũy thừa:

a) $5.5.5.5$

b) 9.9.9.9.9.9.9

c) 7.7.7.7.7

d) $a.a.a.a.a.a.a.a$

Phương pháp:

- Tìm cơ số.

- Tìm số mũ.

Trả lời:

a) 5 . 5. 5 . 5 = 5⁴. (vì trong tích có 4 thừa số 5)

b) 9 . 9 . 9 . 9 . 9 . 9 . 9 = 9⁷. (vì trong tích có 7 thừa số 9)

c) 7 . 7 . 7 . 7 . 7 = 7⁵. (vì trong tích có 5 thừa số 7)

d) a . a . a . a . a . a . a . a = a⁸. (vì trong tích có 8 thừa số a)

Bài 2 trang 25 SGK Toán lớp 6 tập 1 - Cánh Diều

Câu hỏi:

Xác định cơ số, số mũ và tính mỗi lũy thừa sau: ${2^5},{5^2},{9^2},{1^{10}},{10^1}$.

Phương pháp:

- Cơ số là số bên dưới.

- Số mũ là số bên trên.

- Sử dụng định nghĩa lũy thừa tính các lũy thừa.

Trả lời:

+) 2⁵ có cơ số là 2, số mũ là 5 và 

2⁵ = 2 . 2 . 2 . 2 . 2 = 4 . 2 . 2 . 2 = 8 . 2 . 2 = 16 . 2 = 32

+)  5² có cơ số là 5, số mũ là 2 và 5² = 5 . 5 = 25

+) 9² có cơ số là 9, số mũ là 2 và 9² = 9 . 9 = 81

+) 1¹⁰ có cơ số là 1, số mũ là 10  và

1¹⁰  = 1.1.1.1.1.1.1.1.1.1 = 1 

+) 10¹ có cơ số là 10, số mũ là 1 và 10¹ = 10. (một số bất kì lũy thừa 1 thì bằng chính nó).

Bài 3 trang 25 SGK Toán lớp 6 tập 1 - Cánh Diều

Câu hỏi:

Viết các số sau dưới dạng lũy thừa với cơ số cho trước.

a) 81, cơ số 3;

b) 81, cơ số 9;

c) 64, cơ số 2;

d) 100 000 000, cơ số 10.

Phương pháp:

a) Viết 81 thành tích của các số 3 

b) Viết 81 thành tích của các số 9.

c) Viết 64 thành tích của các số 2.

d) - Đếm số các chữ số 0 trong 100 000 000.

- Sử dụng kết quả: ${10^n} = 1\underbrace {0...0}_{n{\rm{ chữ số 0}}}$.

Trả lời:

a) Để viết 81 dưới dạng lũy thừa với cơ số 3, ta tách 81 thành tích của các thừa số 3:

81 = 3 . 27 = 3 . 3 . 9 = 3 . 3 . 3 . 3 = 3⁴. 

Vậy 81 = 3⁴. 

b) Để viết 81 dưới dạng lũy thừa với cơ số 9, ta tách 81 thành tích của các thừa số 9:

81 = 9 . 9 = 9²

Vậy 81 = 9².

c) Để viết 64 dưới dạng lũy thừa với cơ số 2, ta tách 64 thành tích của các thừa số 2:

64 = 2 . 32 = 2 . 2 . 16 = 2 . 2. 2 . 8 = 2 . 2 . 2 . 2 . 2 . 2= 2⁶

Vậy 64 = 2⁶. 

d) Để viết 100 000 000 dưới dạng lũy thừa với cơ số 10, ta tách 100 000 000 thành tích của các thừa số 10:

100 000 000 = 10 . 10 000 000 = 10 . 10 . 1 000 000 

= 10 . 10 . 10 . 100 000 

= 10 . 10 . 10 . 10 . 10 000

= 10 . 10 . 10 . 10 . 10 . 1 000

= 10 . 10 . 10 . 10 . 10 . 10 . 100

= 10 . 10 . 10 . 10. 10 . 10 . 10 . 10

= 10⁸ 

Vậy 100 000 000 = 10⁸. 

Bài 4 trang 25 SGK Toán lớp 6 tập 1 - Cánh Diều

Câu hỏi:

Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa:

a) ${3^4}{.3^5}$;     ${16.2^9}$;    $16.32$;

b) ${12^8}:12$;  $243:{3^4}$;  ${10^9}:10000$.

c) ${4.8^6}{.2.8^3}$;  ${12^2}{.2.12^3}.6$;  ${6^3}{.2.6^4}.3$.

Phương pháp:

a)

- Đưa các thừa số trong tích chưa có dạng lũy thừa về dạng lũy thừa.

- Sử dụng quy tắc nhân hai lũy thừa cùng cơ số.

b)

- Đưa các thừa số trong tích chưa có dạng lũy thừa về dạng lũy thừa.

- Sử dụng quy tắc chia hai lũy thừa cùng cơ số.

c)

- Sử dụng tính chất giao hoán và kết hợp của phép nhân để nhóm các thừa số không là lũy thừa với nhau.

- Nhân các thừa số đó đưa về các lũy thừa.

Trả lời:

a) +) 3⁴. 3⁵ = 3^{4 + 5} = 3⁹. 

+) 16 . 2⁹ = (2 . 2 . 2 . 2) . 2⁹ = 2⁴ . 2⁹ = 2^{4 + 9} = 2¹³.

+) 16 . 32 = 2⁴ . (2 . 2 . 2 . 2 . 2) = 2⁴ . 2⁵ = 2^{4 + 5} = 2⁹.

b) +) 12⁸ : 12 = 12⁸ : 12¹ = 12^{8 - 1} = 12⁷.

+) 243 : 3⁴ = (3. 81) : 3⁴ = (3 . 3 . 27) : 3⁴ = (3 . 3 . 3 . 3. 3) : 3⁴ = 3⁵ : 3⁴ = 3^{5 - 4} =3¹.

+) 10⁹ : 10 000 = 10⁹ : (10 . 1 000) = 10⁹ : (10. 10 . 100) 

= 10⁹ : (10 . 10 . 10 . 10) 

= 10⁹ : 10⁴ = 10^{9 - 4}  = 10⁵.

c) +) 4. 8⁶ . 2 . 8³ 

= 4 . 2 . 8⁶ . 8³ (tính chất giao hoán) 

= (4 . 2) . 8⁶ . 8³ (tính chất kết hợp)

= 8 .  8⁶ . 8³ 

= 8¹ . 8⁶ . 8³ 

= 8^{1 + 6} . 8³ 

= 8⁷ . 8³ = 8^{7 + 3} = 8¹⁰. 

+) 12² . 2 . 12³ . 6 

= (2. 6) . (12² . 12³)  (tính chất giao hoán và kết hợp)

= 12 . 12^{2 + 3} 

= 12¹ . 12⁵ = 12^{1 + 5}  = 12⁶. 

+) 6³ . 2 . 6⁴ . 3 

= (2 . 3) . (6³ . 6⁴) (tính chất giao hoán và kết hợp)

= 6 . 6^{3 + 4} 

= 6¹ . 6⁷ = 6^{1 + 7} = 6⁸. 

Bài 5 trang 25 SGK Toán lớp 6 tập 1 - Cánh Diều

Câu hỏi:

So sánh:

a) ${3^2}$ và 3.2;

b) ${2^3}$ và ${3^2}$;

c) ${3^3}$ và ${3^4}$.

Phương pháp:

- Tính các lũy thừa

- So sánh các cặp số tương ứng.

Trả lời:

a) Ta có: 3² = 3 . 3 = 9 và 3 . 2 = 6 

Vì 9 > 6 nên 3² > 3 . 2 

Vậy 3² > 3 . 2. 

b) Ta có: 2³ = 2 . 2 . 2 = 8 và 3² = 3. 3 = 9 

Vì 8 < 9 nên 2³  < 3²

Vậy 2³ < 3².

c) Ta có: 3³ = 3 . 3 . 3 = 27 và 3⁴ = 3 . 3. 3. 3 = 81 

Vì 27 < 81 nên 3³ < 3⁴ 

Vậy 3³ < 3⁴. 

Bài 6 trang 25 SGK Toán lớp 6 tập 1 - Cánh Diều

Câu hỏi:

Khối lượng của Mặt Trời khoảng ${1988550.10^{21}}$ tấn, khối lượng của Trái Đất khoảng ${6.10^{21}}$

tấn. Khối lượng của Mặt Trời gấp khoảng bao nhiêu lần khối lượng của Trái Đất?

Phương pháp:

*) Lấy khối lượng Mặt Trời khoảng ${1988550.10^{21}}$ tấn.

*) Khối lượng của Mặt Trời gấp khoảng số lần khối lượng của Trái Đất:

   +) Tính $\left( {{{1988550.10}^{21}}} \right):\left( {{{6.10}^{21}}} \right)$ :

         - Chia 1988550 cho 6

         - Kết quả nhận được bằng tích của 2 số tìm được.

Trả lời:

Khối lượng Mặt Trời gấp số lần khối lượng Trái Đất là: 

(1 988 550 . 10²¹) : (6 . 10²¹) = (1 988 550 : 6) . (10²¹ : 10²¹) 

= 331 425 . 1 = 331 425 (lần)

Vậy khối lượng Mặt Trời gấp khoảng 331 425 lần khối lượng Trái Đất.

Bài 7 trang 25 SGK Toán lớp 6 tập 1 - Cánh Diều

Câu hỏi:

Cho biết ${11^2} = 121;{111^2} = 12321$. Hãy dự đoán ${1111^2}$ bằng bao nhiêu. Kiểm tra lại dự đoán

đó.

Phương pháp:

- Nhận xét quy luật của ${11^2};{111^2}$ để dự đoán số ${1111^2}$.

- Sử dụng máy tính bỏ túi để tính ${1111^2}$ và kiểm tra xem mình đã dự đoán đúng chưa.

Trả lời:

Ta có:  11² = 121; 111² = 12 321

Do đó ta dự đoán: 1 111² = 1 234 321

Kiểm tra: 1 111² = 1 111 . 1 111  

Ta có: 

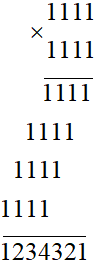
Vậy 1 111² = 1 234 321. 

Giaibaitap.me