Bài 1 trang 56 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
a) Hãy viết các ước của 7 và các ước của 8. Tìm ƯCLN(7,8)
b) Hai số 7 và 8 có nguyên tố cùng nhau không? Vì sao?
c) Tìm BCNN(7,8). So sánh bội chung nhỏ nhất đó với tích của hai số 7 và 8.
a)
- Tìm ước của 7 và 8.
- Tìm ước chung của 7 và 8.
- Ước chung lớn nhất là số lớn nhất trong các ước chung tìm được.
b)
- Hai số nguyên tố cùng nhau là hai số có ước chung lớn nhất bằng 1.
c)
- Phân tích 7 và 8 ra thừa số nguyên tố.
- Chọn ra các thừa số nguyên tố chung và riêng.
- Chọn lũy thừa với số mũ lớn nhất.
- Lấy tích của các lũy thừa đã chọn.
Trả lời:
a) + Để tìm các ước của 7 ta lấy 7 lần lượt chia cho các số tự nhiên từ 1 đến 7, các phép chia hết là: 7 : 1 = 7; 7 : 7 = 1
Do đó: các ước của 7 là: 1; 7
+ Để tìm các ước của 8 ta lấy 8 lần lượt chia cho các số tự nhiên từ 1 đến 8, các phép chia hết là: 8 : 1 = 8; 8 : 2 = 4; 8 : 4 = 2; 8 : 8 = 1.
Các ước của 8 là: 1; 2; 4; 8.
+ Từ đó suy ra ƯC(7, 8) = 1 nên ƯCLN(7, 8) = 1.
b) Vì ƯCLN(7, 8) = 1 (theo câu a) nên hai số 7 và 8 là hai số nguyên tố cùng nhau.
c) Ta có: 7 = 71; 8 = 23
Các thừa số nguyên tố chung và riêng là 7 và 2 với số mũ cao nhất lần lượt là 1 và 3.
Do đó BCNN(7, 8) = 71 . 23 = 56
Mà 7 . 8 = 56
Hay ta nói bội chung nhỏ nhất của hai số nguyên tố cùng nhau 7 và 8 chính bằng tích của hai số 7 và 8.
Bài 2 trang 56 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Quan sát hai thanh sau:
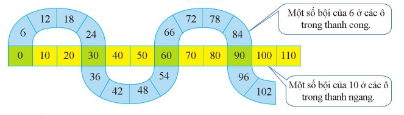
a) Số 0 có phải là bội chung của 6 và 10 không? Vì sao?
b) Viết bốn bội chung của 6 và 10 theo thứ tự tăng dần.
c) Tìm BCNN(6,10)
d) Tìm các bội chung của 6 và 10 mà nhỏ hơn 160.
Phương pháp:
a) Số 0 luôn là bội của mọi số tự nhiên khác 0.
b) Bội chung của 6 và 10 là số bị tô cả 2 màu xanh và vàng.
c) Bội chung nhỏ nhất của 6 và 10 là số khác 0 trong các bội chung của chúng.
d)
- Sử dụng tính chất: Bội chung của 6 và 10 chia hết cho BCNN(6,10).
- Tìm các bội của BCNN(6,10) mà nhỏ hơn 160.
Trả lời:
a) Quan sát hình trên, ta thấy số 0 nằm trên cả 2 thanh, thanh một số bội của 10 (thanh ngang) và thanh một số bội của 6 (thanh cong) nên số 0 là bội chung của 6 và 10.
Mở rộng: Hơn nữa, 0 chia hết cho tất cả các số tự nhiên khác 0 nên 0 là bội của mọi số tự nhiên khác 0.
b) Quan sát hình trên, ta thấy các số 0; 30; 60; 90 (được tô màu đậm hơn) nằm trên cả hai thanh ngang và thanh cong.
Do đó bốn bội chung của 6 và 10 được xếp theo thứ tự tăng dần là: 0; 30; 60; 90.
c) Trong các bội chung trên của 6 và 10, ta thấy 30 là số bé nhất và khác 0.
Do đó nó là bội chung nhỏ nhất của 6 và 10 hay BCNN(6, 10) = 30.
d) Các bội chung của 6 và 10 là các bội của BCNN(6, 10) = 30.
Mà các bội của 30 là: 0; 30; 60; 90; 120; 150; 180;…. (lần lượt nhân 30 với 0, 1, 2, …)
Vậy các bội chung của 6 và 10 nhỏ hơn 160 là: 0; 30; 60; 90; 120; 150.
Bài 3 trang 58 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Tìm bội chung nhỏ nhất của:
a) 7 và 13;
b) 54 và 108;
c) 21, 30, 70.
- Bội chung nhỏ nhất của hai số nguyên tố cùng nhau là tích của hai số đó.
- Cách tìm BCNN:
+ Phân tích các số ra thừa số nguyên tố.
+ Chọn ra các thừa số nguyên tố chung và riêng.
+ Chọn lũy thừa với số mũ lớn nhất.
+ Lấy tích của các lũy thừa đã chọn.
a) Ta có, 7 và 13 đều là các số nguyên tố
Nên 7 và 13 cũng là hai số nguyên tố cùng nhau
Do đó: BCNN(7, 13) = 7 . 13 = 91.
b) Ta có: 54 = 2 . 27 = 2 . 33
108 = 4 . 27 = 22 . 33
Các thừa số nguyên tố chung và riêng của 54 và 108 là 2 và 3, tương ứng với các số mũ lớn nhất lần lượt là 2 và 3
Khi đó: BCNN(54, 108) = 22 . 33 = 4 . 27 = 108.
c) Ta có: 21 = 3 . 7
30 = 3 . 10 = 3 . 2 . 5; 70 = 7. 10 = 7 . 2 . 5
Các thừa số nguyên tố chung và riêng của 21, 30, 70 là 2, 3, 5, 7; chúng đều có số mũ lớn nhất là 1.
Do đó: BCNN(21, 30, 70) = 2 . 3. 5 . 7 = 210.
Bài 4 trang 58 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Thực hiện các phép tính sau:
a) \(\frac{{19}}{{48}} - \frac{3}{{40}}\)
b) \(\frac{1}{6} + \frac{7}{{27}} + \frac{5}{{18}}\)
Phương pháp:
- Chọn mẫu chung là BCNN của các mẫu.
- Tìm thừa số phụ của mỗi mẫu.
- Nhân tử và mẫu của mỗi phân số với mẫu phụ tương ứng.
- Cộng các phân số cùng mẫu.
a)
\(\begin{array}{l}48 = {2^4}{.3^1}\\40 = {2^3}{.5^1}\end{array}\)
Thừa số nguyên tố chung và riêng lần lượt là 2, 3 và 5.
Số mũ lớn nhất của 2 là 4; của 3 là 1; của 5 là 1.
=> \(BCNN\left( {48,40} \right) = {2^4}.3.5 = 240\).
Thừa số phụ của 48 là 240:48=5.
Thừa số phụ của 40 là 240:40=6.
\(\begin{array}{l}\frac{{19}}{{48}} - \frac{3}{{40}}\\ = \frac{{19.5}}{{48.5}} - \frac{{3.6}}{{40.6}}\\ = \frac{{95}}{{240}} - \frac{{18}}{{240}}\\ = \frac{{95 - 18}}{{240}}\\ = \frac{{77}}{{240}}\end{array}\)
b)
\(\begin{array}{l}6 = {2^1}{.3^1}\\27 = {3^3}\\18 = {2^1}{.3^2}\end{array}\)
Thừa số chung và riêng là: 2;3
Số mũ lớn nhất của 2 là 1; của 3 là 3.
=> \(BCNN\left( {6,27,18} \right) = {2.3^3} = 54\).
Thừa số phụ của 6 là 54:6=9
Thừa số phụ của 27 là 54:27=2
Thừa số phụ của 18 là 54:18=3.
\(\begin{array}{l}\frac{1}{6} + \frac{7}{{27}} + \frac{5}{{18}}\\ = \frac{{1.9}}{{6.9}} + \frac{{7.2}}{{27.2}} + \frac{{5.3}}{{18.3}}\\ = \frac{9}{{54}} + \frac{{14}}{{54}} + \frac{{15}}{{54}}\\ = \frac{{9 + 14 + 15}}{{54}}\\ = \frac{{38}}{{54}} = \frac{{19}}{{27}}\end{array}\)
Câu hỏi:
- Bội chung nhỏ nhất của hai số luôn chia hết cho hai số đó.
- Tích của hai số luôn chia hết cho bội chung nhỏ nhất của hai số đó.
- Tìm ước của 45 sao cho 5 nhân với ước đó chia hết cho 45.
Gọi số cần tìm là x
Ta có: BCNN(x, 5) = 45
Mà 45 = 5 . 9 = 5 . 32 ; 5 = 51 và 5 là số nguyên tố nên x và 5 phải là hai số nguyên tố cùng nhau, mà bội chung
nhỏ nhất của hai số nguyên tố cùng nhau chính bằng tích của hai số đó.
Do đó x = 32 = 9.
Vậy số cần tìm là 9.
Bài 6 trang 58 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Câu lạc bộ thể thao của một trường trung học cơ sở có không quá 50 học sinh tham gia. Biết rằng khi chia số
học sinh trong câu lạc bộ đó thành từng nhóm 5 học sinh hoặc 8 học sinh thì vừa hết. Câu lạc bộ thể thao đó có
bao nhiêu học sinh.
Phương pháp:
- Gọi x là tổng số học sinh của CLB.
- Tìm điều kiện cho x.
- Giải điều kiện tìm x.
Gọi a là số học sinh của câu lạc bộ thể thao (a thuộc N* , a ≤ 50)
Vì khi chia số học sinh trong câu lạc bộ đó thành từng nhóm 5 học sinh hoặc 8 học sinh thì vừa hết nên a là bội chung của 5 và 8.
Ta có: 5 = 51; 8 = 23
Do đó: BCNN(5, 8) = 51 . 23 = 5 . 8 = 40
Mà bội chung của 5 và 8 là các bội của BCNN(5, 8) = 40
Nên BC(5, 8) ={0; 40; 80; 120; …}
Vì a ≤ 50 nên a = 40.
Vậy câu lạc bộ thể thao đó có 40 học sinh.
Bài 7 trang 58 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Lịch cập cảng của ba tàu như sau: tàu thứ nhất cứ 10 ngày cập cảng một lần; tàu thứ hai cứ 12 ngày cập cảng một lần; tàu thứ nhất cứ 15 ngày cập cảng một lần. Vào một ngày nào đó, ba tàu cùng nhau cập cảng. Sau ít nhất bao nhiêu ngày thì ba tàu lại cùng nhau cập cảng?
- Số ngày giữa 2 lần cập cảng của tàu thứ nhất phải chia hết cho 10, của tàu thứ hai phải chia hết cho 12, của tàu thứ ba phải chia hết cho 15.
Gọi x là số ngày ít nhất mà ba tàu lại cập cảng cùng nhau. (x thuộc N*)
Vì tàu thứ nhất cứ 10 ngày thì cập cảng một lần nên x là bội của 10.
Tàu thứ hai cứ 12 ngày thì cập cảng một lần nên x là bội của 12.
Tàu thứ ba cứ 15 ngày thì cập cảng một lần nên x là bội của 15.
Do đó x là bội chung của 10, 12 và 15
Mà x là ít nhất nên x là bội chung nhỏ nhất của 10, 12 và 15.
Ta đi tìm BCNN(10, 12, 15)
Ta có: 10 = 2 . 5; 12 = 3 . 4 = 3 . 22; 15 = 3 . 5
Khi đó: BCNN(10, 12, 15) = 22 . 3 . 5 = 4 . 3 . 5 = 60
Hay x = 60
Vậy sau ít nhất 60 ngày thì ba tàu lại cùng nhau cập cảng.
Giaibaitap.me
Giải bài tập trang 59, 60 Bài tập cuối chương - SGK Toán 6 tập 1 Cánh Diều. Bài 5: Tìm BCNN của các số sau a) 72 và 540. b) 28, 49, 64. c) 43 và 53.
Giải bài tập trang 62, 63 Bài 1: Số nguyên âm - SGK Toán 6 tập 1 Cánh Diều. Bài 1 trang 62 Toán lớp 6 Tập 1: a) Đọc các số sau: – 9, – 18. b) Viết các số sau: trừ hai mươi ba; âm ba trăm bốn mươi chín.
Giải bài tập trang 69 Bài 2: Tập hợp các số nguyên - SGK Toán 6 tập 1 Cánh Diều. Bài 1 : Viết các số nguyên biểu thị độ cao so với mực nước biển trong các tình huống sau: a) Máy bay bay ở độ cao 10 000 m; b) Mực nước biển;
Giải bài tập trang 74 Bài 3: Phép cộng các số nguyên - SGK Toán 6 tập 1 Cánh Diều. Bài 2. Trong các phát biểu sau đây, phát biểu nào đúng, phát biểu nào sai? Giải thích.
