Bài 1 trang 51 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Số 1 có phải là ước chung của hai số tự nhiên bất kì không? Vì sao?
Phương pháp:
Số tự nhiên n là ước chung của hai số tự nhiên a và b nếu n vừa là ước của a vừa là ước của b.
Trả lời:
Số 1 là ước chung của hai số tự nhiên bất kì vì tất cả các số tự nhiên đều có ước là 1.
Bài 2 trang 51 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Quan sát hai thanh sau:
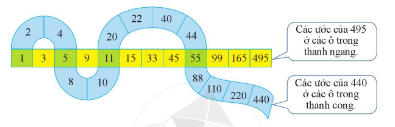
a) Viết tập hợp ƯC(440,495)
b) Tìm ƯCLN(440,495)
Phương pháp:
a) Ước chung của 440 và 495 là các ô giao nhau của 2 thanh.
b) Tìm số lớn nhất trong tập hợp ƯC(440,495).
Trả lời:
a) Quan sát hình vẽ ta thấy
+ Các ước của 440 là: 1; 2; 4; 5; 8; 10; 11; 20; 22; 40; 44; 55; 88; 110; 220; 440
+ Các ước của 495 là: 1; 3; 5; 9; 11; 15; 33; 45; 55; 99; 165; 495
+ Các ước chung của 440 và 495 là: 1; 5; 11; 55.
Vậy ƯC(440, 495) = {1; 5; 11; 55}.
b) Trong các ước chung của 440 và 495, ta thấy 55 là số lớn nhất.
Vậy ƯCLN(440, 495) = 55.
Bài 3 trang 51 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Tìm ước chung lớn nhất của từng cặp số trong 3 số sau đây:
a) 31, 22,34
b) 105, 128, 135
Phương pháp:
a)
- Phân tích 3 số 31, 22, 34 ra thừa số nguyên tố.
- Chọn 2 trong 3 số 31, 22, 34.
- Tìm ƯCLN của 2 số đã chọn.
b)
- Phân tích 3 số 105,128,135 ra thừa số nguyên tố.
- Chọn 2 trong 3 số 105,128,135.
- Tìm ƯCLN của 2 số đã chọn.
Trả lời:
a) + Ta có: 31 là số nguyên tố nên nó chỉ có hai ước là 1 và 31.
22 và 34 không chia hết cho 31
Do đó ta có: ƯCLN(31, 22) = 1 và ƯCLN(31, 34) = 1.
+ Ta còn phải tìm ƯCLN(22, 34), ta phân tích các số 22 và 34 ra thừa số nguyên tố ta được: 22 = 2 . 11; 34 = 2 . 17.
Khi đó thừa số nguyên tố chung của 22 và 34 là 2 với số mũ nhỏ nhất là 1.
Vậy ƯCLN( 22, 34) = 2.
b) Ta phân tích các số 105; 128; 135 ra thừa số nguyên tố, ta có:
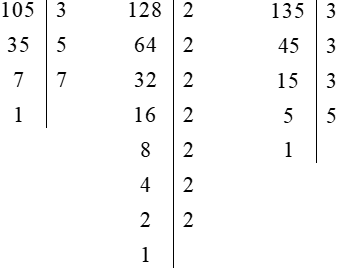
Do đó: 105 = 3 . 5 . 7
128 = 2 . 2 . 2 . 2 . 2 . 2 . 2 = 27
135 = 3 . 3 . 3 . 5 = 33 . 5
+ Hai số 105 và 128 không có thừa số nguyên tố chung nên ƯCLN(105, 128) = 1.
+ Hai số 128 và 135 không có thừa số nguyên tố chung nên ƯCLN(128, 135) = 1.
+ Hai số 105 và 135 có các thừa số nguyên tố chung là 3 và 5.
Số 3 có số mũ nhỏ nhất là 1; số 5 có số mũ nhỏ nhất là 1.
Do đó: ƯCLN(105, 135) = 31 . 51 = 3 . 5 = 15
Vậy ƯCLN(105, 128) = 1; ƯCLN(128, 135) = 1 và ƯCLN(105, 135) = 15.
Bài 4 trang 51 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Tìm ƯCLN(126, 150). Từ đó hãy tìm tất cả các ước chung của 126, 150
Phương pháp:
- Phân tích 3 số 126, 150 ra thừa số nguyên tố.
- Sử dụng tính chất: Ước chung của 126 và 150 là ước của ƯCLN(126,150).
Trả lời:

Do đó: 126 = 2 . 3 . 3 . 7 = 2 . 32 . 7
150 = 2 . 3 . 5 . 5 = 2 . 3 . 52
Các thừa số nguyên tố chung của 126 và 150 là 2 và 3
Số 2 có số mũ nhỏ nhất là 1; số 3 có số mũ nhỏ nhất là 1.
Do đó: ƯCLN(126, 150) = 21 . 31 = 2 . 3 = 6
Lại có 6 có các ước là 1; 2; 3; 6
Ước chung của 126 và 150 là ước của ƯCLN(126, 150) là 1; 2; 3; 6
Hay ƯC(126, 150) = {1; 2; 3; 6}
Vậy ƯCLN(126, 150) = 6; ƯC(126, 150) = {1; 2; 3; 6}.
Bài 5 trang 51 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Rút gọn các phân số sau về phân số tối giản \(\frac{{60}}{{72}};\frac{{70}}{{95}};\frac{{150}}{{360}}\).
Phương pháp:
- Phân tích các số trên tử và mẫu ra thừa số nguyên tố.
- Tìm ƯCLN của tử và mẫu của mỗi phân số.
- Chia cả tử và mẫu cho ƯCLN tìm được.
Trả lời:
+) \(\begin{array}{l}60 = 2.2.3.5 = {2^2}.3.5\\72 = 2.2.2.3.3 = {2^3}{.3^2}\end{array}\)
=>ƯCLN(60,72) = 12.
=>\(\frac{{60}}{{72}} = \frac{60:12}{72:12}= \frac{5}{6}\).
+) \(\begin{array}{l}70 = 2.5.7\\95 = 5.19\end{array}\)
=>ƯCLN (70,95) = 5
=> \(\frac{{70}}{{95}} = \frac{70:5}{95:5}= \frac{{14}}{{19}}\).
+) \(\begin{array}{l}150 = {2.3.5^2}\\360 = {2^3}{.3^2}.5\end{array}\)
=> ƯCLN(150,360)=2.3.5=30
=> \(\frac{{150}}{{360}} = \frac{150:30}{360:30}= \frac{5}{{12}}\).
Bài 6 trang 51 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Phân số \(\frac{4}{9}\) bằng các phân số nào trong các phân số sau: \(\frac{{48}}{{108}};\frac{{80}}{{180}};\frac{{60}}{{130}};\frac{{135}}{{270}}\).
Phương pháp:
- Rút gọn các phân số đã cho về phân số tối giản.
- Nếu phân số tối giản là \(\frac{4}{9}\) thì phân số ban đầu bằng \(\frac{4}{9}\).
Trả lời:
ƯCLN(48,108)=12
=>\(\frac{{48}}{{108}} = \frac{4}{9}\)
ƯCLN(80,180)=20
=> \(\frac{{80}}{{180}} = \frac{4}{9}\)
ƯCLN(60,130)=10
=>\(\frac{{60}}{{130}} = \frac{6}{{13}}\)
ƯCLN(135,270)=135
=>\(\frac{{135}}{{270}} = \frac{1}{2}\)
Phân số \(\frac{4}{9}\) bằng các phân số \(\frac{{48}}{{108}};\frac{{80}}{{180}}\).
Bài 7 trang 51 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Một nhóm gồm 24 bạn nữ và 30 bạn nam tham gia một số trò chơi. Có thể chia các bạn thành nhiều nhất bao
nhiêu đội chơi sao cho số bạn nam cũng như số bạn nữ được chia đều vào các đội?
- Gọi số đội được chia.
- Số độ phải là ƯCLN của 24 và 30.
- Tìm ƯCLN(24,30).
Giả sử a là số đội chơi được chia. (a thuộc N*)
Vì a là lớn nhất (phải chia nhiều đội nhất) và số bạn nam cũng như số bạn nữ được chia đều vào các đội nên khi
đó a là ước chung lớn nhất của 24 và 30.
Ta có: 24 = 3 . 8 = 3 . 23 ; 30 = 3 . 10 = 3 . 2 . 5
(Các thừa số chung là 2; 3 và đều có số mũ nhỏ nhất là 1)
Khi đó: ƯCLN(24, 30) = 2 . 3 = 6 hay a = 6.
Vậy có thể chia các bạn nhiều nhất thành 6 đội.
Bài 8 trang 51 SGK Toán lớp 6 tập 1 - Cánh Diều
Câu hỏi:
Một khu đất có dạng hình chữ nhật với chiều dài 48m, chiều rộng 42m. Người ta muốn chia khu đất ấy thành
những mảnh hình vuông bằng nhau (với độ dài cạnh đo theo đơn vị mét là số tự nhiên) để trồng các loại rau. Có
thể chia được bằng bao nhiêu cách? Với cách chia nào thì cạnh của mảnh đất hình vuông là lớn nhất và bằng bao
nhiêu?
- Gọi số cách chia mảnh đất và độ dài cạnh hình vuông lớn nhất.
- Tìm số ước chung của 48 và 42: Số cách chia.
- Tìm ƯCLN(42, 48): độ dài cạnh lớn nhất.
Gọi: a là số cách chia mảnh đất thành các mảnh hình vuông bằng nhau
b (m) là độ dài cạnh của mảnh đất hình vuông được chia theo cách chia lớn nhất a,b thuộc N*
Theo yêu cầu bài ra thì khi đó:
+ a là số các ước chung của 48 và 42
+ b là ước chung lớn nhất của 48 và 42
Ta có: 42 = 2 . 21 = 2 . 3 . 7
48 = 16 . 3 = 24 . 3
Do đó: ƯCLN(42, 48) = 2 . 3 = 6 hay b = 6 m
Mà Ư(6) = {1; 2; 3; 6) Nên ƯC(42, 48) = {1; 2; 3; 6}
Do đó có 4 ước chung của 42 và 48 hay a = 4.
Vậy:
+ Số cách chia thành những mảnh hình vuông bằng nhau là 4 cách.
+ Với cách chia có độ dài cạnh là 6m thì cạnh của mảnh đất hình vuông là lớn nhất.
Giaibaitap.me
Giải bài tập trang 57, 58 Bài 13: Bội chung và bội chung nhỏ nhất - SGK Toán 6 tập 1 Cánh Diều. Bài 1: a) Hãy viết các ước của 7 và các ước của 8. Tìm ƯCLN(7, 8). b) Hai số 7 và 8 có nguyên tố cùng nhau hay không? Vì sao?
Giải bài tập trang 59, 60 Bài tập cuối chương - SGK Toán 6 tập 1 Cánh Diều. Bài 5: Tìm BCNN của các số sau a) 72 và 540. b) 28, 49, 64. c) 43 và 53.
Giải bài tập trang 62, 63 Bài 1: Số nguyên âm - SGK Toán 6 tập 1 Cánh Diều. Bài 1 trang 62 Toán lớp 6 Tập 1: a) Đọc các số sau: – 9, – 18. b) Viết các số sau: trừ hai mươi ba; âm ba trăm bốn mươi chín.
Giải bài tập trang 69 Bài 2: Tập hợp các số nguyên - SGK Toán 6 tập 1 Cánh Diều. Bài 1 : Viết các số nguyên biểu thị độ cao so với mực nước biển trong các tình huống sau: a) Máy bay bay ở độ cao 10 000 m; b) Mực nước biển;
