Bài 2.17 trang 41 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi: 

Phân tích các số sau ra thừa số nguyên tố: 70; 115. 

Phương pháp: 

Phân tích theo sơ đồ cây hoặc sơ đồ cột, sau đó viết gọn kết quả

Lời giải:

+) 70

Vậy 70 = 2.5.7

+) 115

Vậy 115 = 5.23

Bài 2.18 trang 41 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi: 

Kết quả phân tích các số 120; 102 ra thừa số nguyên tố của bạn Nam như sau:

120 = 2.3.4.5 ; 102 = 2.51.

Theo em, kết quả của Nam đúng hay sai? Nếu sai, em hãy sửa lại cho đúng.

Phương pháp:

Quan sát xem các số trong tích đã là các thừa số nguyên tố chưa? Từ đó kết luận

Lời giải: 

+) Với cách phân tích 120 = 2.3.4.5 ta thấy 4 là hợp số vì có 3 ước là: 1, 2, 4 nên kết quả của Nam là sai.

Sửa lại: 120 = 2 . 2 . 2 . 3 . 5 = 23.3.5

+) Với cách phân tích 102 = 2.51 ta thấy 51 là hợp số vì có 4 ước là: 1, 3, 17, 51 nên kết quả của Nam là sai.

Sửa lại: 102 = 2 . 3 . 17

Bài 2.19 trang 41 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi:

Các khẳng định sau đúng hay sai? Vì sao?

a) Ước nguyên tố của 30 là 5 và 6;

b) Tích của hai số nguyên tố bất kì luôn là số lẻ;

c) Ước nguyên tố nhỏ nhất của số chẵn là 2;

d) Mọi bội của 3 đều là hợp số;

e) Mọi số chẵn đều là hợp số.

Phương pháp: 

Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.

Lời giải:

a) Sai. Vì số 6 có 4 ước là 1; 2; 3; 6 nên 6 là hợp số.

b) Sai. Vì ví dụ hai số nguyên bất kì là: 2 và 3 nhưng tích 2 . 3 = 6 là số chẵn 

c) Đúng. Vì 2 là số nguyên tố nhỏ nhất và là số chẵn duy nhất

d) Sai. Vì 3 là bội của 3 nhưng 3 là số nguyên tố

e) Sai. Vì 2 là số chẵn nhưng 2 là số nguyên tố.

Bài 2.20 trang 42 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi: 

Kiểm tra xem các số sau là số nguyên tố hay hợp số bằng cách dùng dấu hiệu chia hết hoặc tra bảng số nguyên tố:

89; 97; 125; 541; 2013; 2018.

Phương pháp:

Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.

Lời giải:

Các số nguyên tố là: 89 ; 97 ; 541 vì mỗi số này chỉ có 2 ước là 1 và chính nó

Các hợp số là: 125 ; 2 013; 2 018 vì mỗi số này có nhiều hơn 2 ước ( ngoài 1 và chính nó, 125 còn có ước là 5; 2013 còn có ước là 3; 2018 còn có ước là 2).

Bài 2.21 trang 42 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi: 

Hãy phân tích A ra thừa số nguyên tố: A = 4⁴.9⁵

Phương pháp:

Đưa A về tích các lũy thừa cơ số 2 và 3.

Lời giải: 

A = 4⁴.9⁵

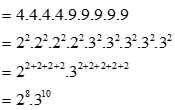
Bài 2.22 trang 42 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi: 

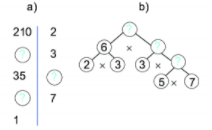
Tìm các số còn thiếu trong các sơ đồ phân tích một số ra thừa số nguyên tố sau:

Phương pháp:

Phân tích các số ra thừa số nguyên tố theo sơ đồ cây và sơ đồ cột

Lời giải: 

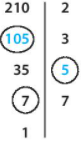
a)

+) Ta có 210 : 2 = 105

              105 : 3 = 35

                35 : 5 = 7

                  7 : 7 = 1

Vậy: 

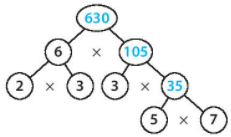
b)

+) Ta có: 5 x 7 = 35

             35 x 3 = 105

            105 x 6 = 6

Vậy:

Bài 2.23 trang 42 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi: 

Một lớp có 30 học sinh. Cô giáo muốn chia lớp thành các nhóm để thực hiện các dự án học tập nhỏ. Biết rằng, các nhóm đều có số người bằng nhau và có nhiều hơn 1 người trong mỗi nhóm. Hỏi mỗi nhóm có thể có bao nhiêu người?

Phương pháp: 

Phân tích 30 ra thừa số nguyên tố sau đó lập bảng.

Lời giải:

Phân tích 30 ra thừa số nguyên tố ta được: 30 = 2.3.5 

Vì cô giáo muốn chia lớp 30 học sinh thành các nhóm nên số nhóm là ước của 30

Ư(30) = { 1; 2; 3; 5; 6; 10; 15; 30}

Ta có bảng sau:

Do mỗi nhóm có nhiều hơn 1 người nên số người trong một nhóm là 2; 3; 5; 6; 10; 15; 30

Vậy mỗi nhóm có thể có 2; 3; 5; 6; 10; 15 hoặc 30 người.

Bài 2.24 trang 42 SGK Toán lớp 6 tập 1 - KNTT

Câu hỏi: 

Trong nghi lễ thượng cờ lúc 6 giờ sáng và hạ cờ lúc 21 giờ hằng ngày ở Quảng trường Ba Đình, đội tiêu binh có 34 người gồm 1 sĩ quan chỉ huy đứng đầu và 33 chiến sĩ. Hỏi có bao nhiêu cách sắp xếp 33 chiến sĩ thành các hàng sao cho mỗi hàng có số người như nhau?

Phương pháp:

Tìm các ước của 33 để suy ra số cách sắp xếp.

Lời giải:

Ta có: 33 = 3 . 11

Vì xếp 33 chiến sĩ thành các hàng thì số hàng là ước của 33

Ư(33) = {1; 3; 11; 33}

Với số hàng là 1 thì số người mỗi hàng là: 33 : 1 = 33 (người)

Với số hàng là 3 thì số người mỗi hàng là: 33 : 3 = 11 (người)

Với số hàng là 11 thì số người mỗi hàng là: 33 : 11 = 3 (người)

Với số hàng là 33 thì số người mỗi hàng là: 33 : 33 = 1 (người)

Vậy có 4 cách cách sắp xếp 33 chiến sĩ thành các hàng.

Giaibaitap.me