Câu 9 trang 138 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC). Tìm góc bằng góc B.

Giải

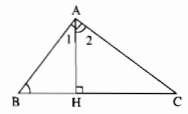
Có thể tìm góc B bằng hai cách:

*Cách 1

Ta có \(\widehat {{A_1}} + \widehat {{A_2}} = \widehat {BAC} = 90^\circ \)                          (1)

Vì ∆AHB vuông tại H nên:

\(\widehat B + \widehat A = 90^\circ \) (tính chất tam giác vuông)         (2)

Từ (1) và (2) suy ra: \(\widehat B = \widehat {{A_2}}\)

*Cách 2

Vì ∆ABC vuông tại A nên: 

\(\widehat B + \widehat C = 90^\circ \) (tính chất tam giác vuông)             (1)

Vì ∆AHC vuông tại H nên

\(\widehat {{A_2}} + \widehat C = 90^\circ \) (tính chất tam giác vuông)          (2)

Từ (1) và (2) suy ra: \(\widehat B = \widehat {{A_2}}\).

Câu 10 trang 138 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho hình dưới:

a) Có bao nhiêu tam giác vuông trong hình?

b) Tính số đo các góc nhọn ở các đỉnh C, D, E.

Giải

a) Có năm tam giác vuông trong hình:

               ∆ABC vuông tại B

               ∆CBD vuông tại B

               ∆EDA vuông tại D

               ∆DCAvuông tại C

               ∆DCEvuông tại C

b) ∆ABC vuông tại B, suy ra:

\(\widehat A + \widehat {ACB} = 90^\circ \) (tính chất tam giác vuông)

\(\eqalign{
& \Rightarrow \widehat {ACB} = 90^\circ - \widehat A = 90^\circ - 40^\circ = 50^\circ \cr
& \widehat {ACB} + \widehat {BC{\rm{D}}} = \widehat {AC{\rm{D}}} = 90^\circ \cr
& \Rightarrow \widehat {BC{\rm{D}}} = 90^\circ - \widehat {ACB} = 90^\circ - 50^\circ = 40^\circ \cr} \)

∆ACD vuông tại C, suy ra:

\(\widehat A + \widehat {C{\rm{D}}A} = 90^\circ \) (tính chất tam giác vuông)

\(\eqalign{
& \Rightarrow \widehat {C{\rm{D}}A} = 90^\circ - \widehat A = 90^\circ - 40^\circ = 50^\circ \cr
& \widehat {C{\rm{D}}A} + \widehat {C{\rm{D}}E} = \widehat {A{\rm{D}}E} = 90^\circ \cr
& \Rightarrow \widehat {C{\rm{D}}E} = 90^\circ - \widehat {C{\rm{D}}A} = 90^\circ - 50^\circ = 40^\circ \cr} \)

∆DEA vuông tại D, suy ra:

\(\widehat A + \widehat E = 90^\circ \) (tính chất tam giác vuông)

\( \Rightarrow \widehat E = 90^\circ  - \widehat A = 90^\circ  - 40^\circ  = 50^\circ \)

Câu 11 trang 138 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC có \(\widehat B = 70^\circ ,\widehat C = 30^\circ \). Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC (H ∈ BC).

a) Tính \(\widehat {BAC}\) 

b) Tính \(\widehat {A{\rm{D}}H}\)

c) Tính \(\widehat {HA{\rm{D}}}\)

Giải

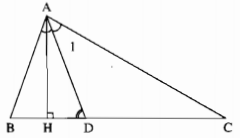
a) Trong ∆ABC, ta có:

\(\widehat {BAC} + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong tam giác)

Mà \(\widehat B = 70^\circ ;\widehat C = 30^\circ \left( {gt} \right)\)

Suy ra: \(\widehat {BAC} + 70^\circ  + 30^\circ  = 180^\circ \)

Vậy \(\widehat {BAC} = 180^\circ  - 70^\circ  - 30^\circ  = 80^\circ \)

b) Ta có: \(\widehat {{A_1}} = {1 \over 2}\widehat {BAC} = {1 \over 2}.80^\circ  = 40^\circ \) (Vì AD là tia phân giác của \(\widehat {BAC}\))

Trong ∆ADC ta có \(\widehat {A{\rm{D}}H}\) là góc ngoài tại đỉnh D.

Do đó: \(\widehat {A{\rm{D}}H} = \widehat {{A_1}} + \widehat C\) (tính chất góc ngoài của tam giác)

Vậy \(\widehat {A{\rm{D}}H} = 40^\circ  + 30^\circ  = 70^\circ \)

c) ∆ADH vuông tại H nên:

\(\widehat {HA{\rm{D}}} + \widehat {A{\rm{D}}H} = 90^\circ \) (tính chất tam giác vuông)

\( \Rightarrow \widehat {HA{\rm{D}}} = 90^\circ  - \widehat {A{\rm{D}}H} = 90^\circ  - 70^\circ  = 20^\circ \)

Câu 12 trang 138 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Tính \(\widehat {BIC}\) biết rằng:

a) \({\rm{}}\widehat B = 80^\circ ,\widehat C = 40^\circ \)

b) \(\widehat A = 80^\circ \)

c) \(\widehat A = m^\circ \)

Giải

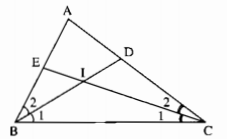
a) Ta có

\(\widehat {{B_1}} = {1 \over 2}\widehat {ABC} = {1 \over 2}.80^\circ  = 40^\circ \) (vì BD là tia phân giác của \(\widehat {ABC}\))

\(\widehat {{C_1}} = {1 \over 2}\widehat {ACB} = {1 \over 2}.40^\circ  = 20^\circ \) (vì CE là tia phân giác của \(\widehat {ACB}\))

Trong ∆IBC, ta có: \(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng 3 góc trong tam giác)

\(\widehat {BIC} = 180^\circ  - \left( {\widehat {\widehat {{B_1}} + {C_1}}} \right) = 180^\circ  - \left( {40^\circ  + 20^\circ } \right) = 120^\circ \)

b) Ta có:

\(\widehat {{B_1}} = {1 \over 2}\widehat B\) (vì BD là tia phân giác \(\widehat B\))

\(\widehat {{C_1}} = {1 \over 2}\widehat C\) (vì CE là tia phân giác \(\widehat C\))

Trong ∆ABC, ta có:

\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong tam giác)

Suy ra \(\widehat B + \widehat C = 180^\circ  - \widehat A = 180^\circ  - 80^\circ  = 100^\circ \)

Trong ∆IBC, ta có: \(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \)

Vậy \(\widehat {BIC} = 180^\circ  - \left( {\widehat {{B_1}} + \widehat {{C_1}}} \right) = 180^\circ  - {{\widehat B + \widehat C} \over 2} = 180^\circ  - {{100^\circ } \over 2} = 130^\circ \)

c) Ta có: \(\widehat B + \widehat C = 180 - m^\circ \)

Vậy \(\widehat {BIC} = 180^\circ  - {{180^\circ  - m^\circ } \over 2} = 180^\circ  - 90^\circ  + {{m^\circ } \over 2} = 90^\circ  + {{m^\circ } \over 2}\)

Giaibaitap.me