Câu 74 trang 51 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của tam giác ABC, AHB, AHC.
Giải
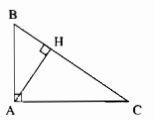
∆ABC có \(\widehat {BAC} = 90^\circ \)
CA là đường cao xuất phát từ đỉnh C. BA là đương cao xuất phát từ đỉnh B. Giao điểm của hai đường này là A. Vậy A là trực tâm của ∆ABC.
∆AHB có \(\widehat {AHB} = 90^\circ \)
AH là đường cao xuất phát từ đỉnh A; BH là là đường cao xuất phát từ đỉnh B. Giao điểm của hai đường này là H. Vậy H là trực tâm của ∆AHB
∆AHC có \(\widehat {AHC} = 90^\circ \)
AH là đường cao xuất phát từ đỉnh A; CH là đường cao xuất phát từ đỉnh C. Giao điểm của hai đường này là H
Vậy H là trực tâm của ∆AHC.
Câu 75 trang 51 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho hình sau. Có thể khẳng định rằng các đường thẳng AC, BD, KE cùng đi qua một điểm hay không? Vì sao?
Giải
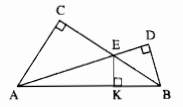
Trong ∆AEB ta có:
\(AC \bot {\rm{E}}B\) nên AC là đường cao xuất phát từ đỉnh A.
\(B{\rm{D}} \bot A{\rm{E}}\) nên BD là đường cao xuất phát từ đỉnh B.
\(EK \bot AB\) nên EK là đường cao xuất phát từ đỉnh E.
Theo tính chất ba đường cao trong tam giác nên các đường thẳng AC, BD và EK cùng đi qua một điểm.
Câu 76 trang 51 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho tam giác ABC cân tại A, đường trung tuyến AM. Qua kẻ đường thẳng d vuông góc với AM. Chứng minh rằng d song song với BC.
Giải
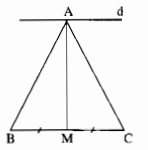
∆ABC cân tại A, AM là đường trung tuyến nên AM cũng là đường cao.
\(\eqalign{
& {\rm{AM}} \bot {\rm{BC}} \cr
& {\rm{d}} \bot {\rm{AM}}\left( {gt} \right) \cr} \)
Suy ra: d // BC (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba).
Câu 77 trang 51 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Kẻ đường cao AE của ∆ABC, đường cao AF của ∆ACD. Chứng minh rằng \(\widehat {EAF} = 90^\circ \)
Giải
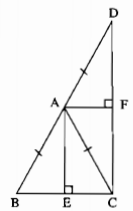
∆ABC cân tại A.
\(A{\rm{E}} \bot BC\left( {gt} \right)\)
Ta có: AE là đường cao nên AE cũng là đường phân giác của \(\widehat {BAC}\)
∆ADC cân tại A.
\({\rm{AF}} \bot {\rm{DC}}\left( {gt} \right)\)
Ta có: AF là đường cao nên AF cũng là đường phân giác của \(\widehat {CA{\rm{D}}}\)
Mà \(\widehat {BAC}\) và \(\widehat {CA{\rm{D}}}\) là hai góc kề bù.
Suy ra: \(A{\rm{E}} \bot {\rm{AF}}\)
Giaibaitap.me
Giải bài tập trang 51 bài 9 tính chất ba đường cao của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 78: Cho tam giác ABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC...
Giải bài tập trang 52 bài 9 tính chất ba đường cao của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 9.4: Cho tam giác nhọn ABC cân tại đỉnh A. Hai đường cao xuất phát từ đỉnh B và đỉnh C cắt nhau tại M...
Giải bài tập trang 52, 53 bài ôn tập chương III Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 82: Cho Tam giác ABC có AB < AC. Trên tia dối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA...
Giải bài tập trang 53 bài ôn tập chương III Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 86: Cho hình sau trong đó G là trọng tâm của tam giác ABC. Chứng minh rằng...
