Câu 16 trang 139 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC có \(\widehat A = 90^\circ \), kẻ AH vuông góc với BC (H ∈ BC). Các tia phân giác của các góc \(\widehat C\) và \(\widehat {BAH}\) cắt nhau ở I. Chứng minh rằng: \(\widehat {AIC} = 90^\circ \)

Giải

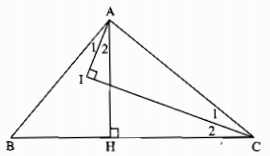
Ta có: \(AH \bot BC\left( {gt} \right) \Rightarrow \Delta AHB\) vuông tại H

Trong tam giác vuông AHB ta có: \(\widehat {AHB} = 90^\circ \)

\( \Rightarrow \widehat B + \widehat {BAH} = 90^\circ \left( 1 \right)\)

Trong tam giác vuông ABC, ta có: \(\widehat {BAC} = 90^\circ \)

\( \Rightarrow \widehat B + \widehat C = 90^\circ \left( 2 \right)\)

Từ (1) và (2) suy ra: \(\widehat {BAH} = \widehat C\)

\(\eqalign{
& \widehat {{A_1}} = \widehat {{A_2}} = {1 \over 2}\widehat {BAH}\left( {gt} \right) \cr
& \widehat {{C_1}} = \widehat {{C_2}} = {1 \over 2}\widehat C\left( {gt} \right) \cr} \)

Suy ra: \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{C_1}} = \widehat {{C_2}}\)

\(\widehat {{A_1}} + \widehat {IAC} = \widehat {BAC} = 90^\circ \)

Suy ra: \(\widehat {{C_1}} + \widehat {IAC} = 90^\circ \)

Trong ∆ AIC ta có: \(\widehat {IAC} + \widehat {{C_1}} = 90^\circ \)

Vậy \(\widehat {AIC} = 90^\circ \)

Câu 17 trang 139 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Chứng minh rằng nếu một đường thẳng cắt hai đường thẳng song song thì hai tia phân giác của cặp góc trong cùng phía vuông góc với nhau.

Giải

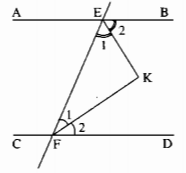
Giả sử đường thẳng AB // CD cắt đường thẳng EF tại E và F

Ta có: \(\widehat {BEF} + \widehat {EFD} = 180^\circ \) (hai góc trong cùng phía)

\(\eqalign{
& \widehat {{E_1}} = {1 \over 2}\widehat {{\rm{BEF}}}\left( {gt} \right) \cr
& \widehat {{F_1}} = {1 \over 2}\widehat {EFD}\left( {gt} \right) \cr} \)

\( \Rightarrow \widehat {{E_1}} + \widehat {{F_1}} = {1 \over 2}\left( {\widehat {{\rm{BEF}}} + \widehat {EFD}} \right) = 90^\circ \)

Trong ∆EKF, ta có:

\(\widehat {EKF} = 180^\circ  - \left( {\widehat {{E_1} + \widehat {{F_1}}}} \right) = 180^\circ  - 90^\circ  = 90^\circ \)

Vậy \(EK \bot FK\).

Câu 18 trang 139 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC có \(\widehat B - \widehat C = 20^\circ \). Tia phân giác của góc A cắt BC ở D. Tính số đo các góc \(\widehat {A{\rm{D}}C},\widehat {A{\rm{D}}B}\).

Giải

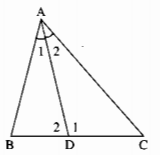
Trong ∆ABD ta có \(\widehat {{D_1}}\) là góc ngoài tại đỉnh D.

\(\widehat {{D_1}} = \widehat B + \widehat {{A_1}}\) (tính chất góc ngoài của tam giác)

Trong ∆ADC ta có \(\widehat {{D_2}}\) là góc ngoài tại đỉnh D

\(\widehat {{D_2}} = \widehat C + \widehat {{A_2}}\) (tínhchất góc ngoài của tam giác)

Ta có: \(\widehat B > \widehat C\left( {gt} \right);\widehat {{A_1}} = \widehat {{A_2}}\left( {gt} \right)\)

\( \Rightarrow \widehat {{D_1}} - \widehat {{D_2}} = \left( {\widehat B + \widehat {{A_1}}} \right) - \left( {\widehat C + \widehat {{A_2}}} \right)\)

\( = \widehat B - \widehat C = 20^\circ \)

\(\widehat {{D_1}} + \widehat {{D_2}} = 180^\circ \) (hai góc kề bù)

\(\eqalign{
& \Rightarrow \widehat {{D_1}} = \left( {180^\circ + 20^\circ } \right):2 = 100^\circ \cr
& \Rightarrow \widehat {{D_2}} = 100^\circ - 20^\circ = 80^\circ \cr} \)

Vậy \(\widehat {A{\rm{D}}C} = 100^\circ ;\widehat {A{\rm{D}}B} = 80^\circ \)

Giaibaitap.me