Câu 82 trang 52 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho Tam giác ABC có AB < AC. Trên tia dối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA.

a) Hãy so sánh các góc AMB và ANC.

b) Hãy so sánh các độ dài AM và AN.

Giải

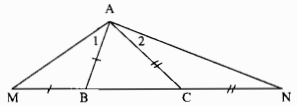
Trong ∆ABC có AB < AC

\( \Rightarrow \) \(\widehat {ABC} = \widehat {ACB}\) (đối diện cạnh lớn hơn là góc lớn hơn)      (1)

Ta có:   AB = BM (gt)

\( \Rightarrow \) ∆ABM cân tại B

\( \Rightarrow \) \(\widehat M = \widehat {{A_1}}\) (tính chất tam giác cân)

Trong ∆ABM ta có có góc ngoài tại đỉnh B

\(\widehat {ABC} = \widehat M + \widehat {{A_1}}\)

Suy ra: \(\widehat M = {1 \over 2}\widehat {ABC}\)                (2)

Ta có:          AC = CN (gt)

\( \Rightarrow \) ∆CAN cân tại C

\( \Rightarrow \) \(\widehat N = \widehat {{A_2}}\) (tính chất tam giác cân)

Trong ∆CAN ta có \(\widehat {ACB}\) là góc ngoài tại đỉnh C.

\( \Rightarrow \widehat {ACB} = \widehat N + \widehat {{A_2}}\)

Suy ra: \(\widehat N = {1 \over 2}\widehat {ACB}\)           (3)

Từ (1), (2) và (3) suy ra: \(\widehat M > \widehat N\)

b) Trong ∆AMN ta có: \(\widehat M > \widehat N\)

Suy ra:  AN > AM (đối diện góc lớn hơn là cạnh lớn hơn)

Câu 83 trang 52 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC có AB < AC, đường cao AH. Chứng minh rằng:

HB < HC, \(\widehat {HAB} < \widehat {HAC}\) (xét hai trường hợp: \(\widehat B\) nhọn và \(\widehat B\) tù).

Giải

a)

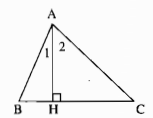
Trường hợp: \(\widehat B < 90^\circ \)

Đường xiên AB < AC nên hình chiếu HB < HC

Trong ∆ABC ta có: AB  < AC

\( \Rightarrow \widehat B < \widehat C\) (đối diện cạnh lớn hơn là góc lớn hơn)

Trong ∆AHB có \(\widehat {AHB} = 90^\circ \)

\( \Rightarrow \widehat B + \widehat {HAC} = 90^\circ \) (tính chất tam giác vuông)       (1)

Trong ∆AHC có \(\widehat {AHC} = 90^\circ \)

\( \Rightarrow \widehat C + \widehat {HAC} = 90^\circ \) (tính chất tam giác vuông)         (2)

Từ (1) và (2) suy ra: \(\widehat B + \widehat {HAB} = \widehat C + \widehat {HAC}\)

Mà \(\widehat B > \widehat C\) nên \(\widehat {HAB} < \widehat {HAC}\)

b)

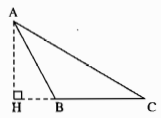
Nếu \(90^\circ  < \widehat B < 180^\circ \) điểm B nằm giữa H và C.

\(\widehat {HAC} = \widehat {HAB} + \widehat {BAC}\)

\( \Rightarrow \widehat {HAB} < \widehat {HAC}\)

Câu 84 trang 52 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài 1cm, 2cm, 3cm, 4cm, 5cm.

Giải

1 = 3 – 2 = 4 – 3 = 5 – 4

Nên trong 3 cạnh của tam giác không có cạnh nào có độ dài 1cm.

Nếu cạnh nhỏ nhất là 2cm

4 – 3 < 2 <  4 + 3; 5 – 4 < 2 < 5 + 4

Thì 2 cạnh kia là 3cm và 4cm hoặc 4cm và 5cm.

Nếu cạnh nhỏ nhất là 3cm

5 – 4 < + < 5 + 4; 3 = 5 – 2; 3 > 4 – 2

Như vậy hai cạnh kia là 5 và 4.

Không có trường hợp cạnh nhỏ nhất là 4cm.

Vậy ta có thể vẽ được 3 tam giác có ba cạnh là:

2cm; 3cm; 4cm 

2cm; 4cm; 5cm 

3cm; 4cm; 5cm 

Câu 85 trang 53 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho bốn điểm A, B, C, D như hình dưới. Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất.

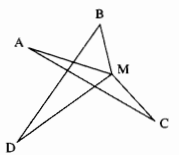
Giải

Với M là điểm bất kỳ.

Ta có M không trùng với giao điểm của AC và BD

Trong ∆MBD ta có:

MB + MD > BD (bất đẳng thức tam giác)

Nếu M trùng với giao điểm  AC và BD

\( \Rightarrow \) MA + MC = AC

MB + MD = BD

Vậy        MA + MC ≥ AC

               MB + MD ≥ BD

(dấu bằng xảy ra khi M trùng với giao điểm của AC và BD)

\( \Rightarrow \) MA + MB + MC  + MD ≥ AC + BD

Vậy MA + MB + MC + MD = AC + BD bé nhất khi đó M là giao điểm của AC và BD

Giaibaitap.me