Câu 86 trang 53 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho hình sau trong đó G là trọng tâm của tam giác ABC. Chứng minh rằng:
a) \({S_{AGC}} = 2{{\rm{S}}_{GMC}}\)
b) \({S_{Gmb}} = {S_{GMC}}\)
c) \({S_{AGB}} = {S_{AGC}} = {S_{BGC}}\)
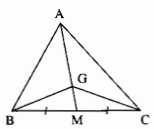
Giải
a) G là trọng tâm của ∆ABC
\( \Rightarrow \) GA = 2GM (tính chất đường trung tuyến)
∆AGC và ∆GMC có chung đường cao kẻ từ đỉnh C đến AM.
Cạnh đáy GA = 2GM
Chiều cao chung của hai tam giác
Suy ra: \({S_{AGC}} = 2{{\rm{S}}_{GMC}}\) (1)
b) ∆GMB và ∆GMC có cạnh đáy MB = MC, chung chiều cao kẻ từ đỉnh G đến cạnh BC
\({S_{Gmb}} = {S_{GMC}}\) (2)
c) Hai tam giác AGB và GMB có chung chiều cao kẻ từ đỉnh B đến cạnh AM.
AG = 2GM (chứng minh trên)
Suy ra:
\(\eqalign{
& {S_{AGB}} = 2{{\rm{S}}_{GMB}}\left( 3 \right) \cr
& {S_{BGC}} = {S_{GMB}} + {S_{GMC}} = 2{S_{GMB}}\left( 4 \right) \cr} \)
Từ (1), (2) và (3) suy ra: \({{\rm{S}}_{AGC}} = {S_{AGB}} = {S_{BGC}}\)
Câu 87 trang 53 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy.
a) Hãy tìm điểm M nằm trong góc xOy, cách đều Ox, Oy và cách đều A, B.
b) Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a?
Giải
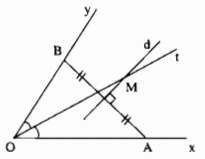
a) - Điểm nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên nó thuộc tia phân giác Ot của \(\widehat {xOy}\).
- Điểm cách đều 2 điểm A và B thuộc đường thẳng d là đường trung trực của AB
Vậy M là giao điểm của dường trung trực của đoạn thẳng AB và tia phân giác Ot của \(\widehat {xOy}\)
b) Nếu OA = OB
\( \Rightarrow \) ∆OAB cân tại O
Tia phân giác của \(\widehat {xOy}\) cũng là đường trung trực của AB. Vậy bất kỳ điểm M nào nằm trên tia phân giác của \(\widehat {xOy}\) đều thỏa mãn điều kiện câu a.
Câu 88 trang 53 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho góc xOy khác góc bẹt. Dùng một chiếc thước thẳng có chia khoảng, hãy nêu cách vẽ tia phân giác của góc xOy.
Giải
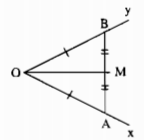
- Dùng thước chia khoảng, trên Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB.
- Nối AB
- Dùng thước chia khoảng, đo đoạn AB, lấy trung điểm M của AB.
- Kẻ tia OM.
Ta có ∆OAB cân tại O, OM là đường trung tuyến nên OM cũng là đường phân giác \(\widehat {AOB}\).
Vậy OM là tia phân giác của \(\widehat {xOy}\).
Giaibaitap.me
Giải bài tập trang 53, 54 bài ôn tập chương III Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 89: Cho hình 20 trong đó giao điểm O của hai đường thẳng a và a nằm ngoài phạm vi tờ giấy...
Giải bài tập trang 54 bài ôn tập chương III Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu III.1: Chứng minh rằng trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ một đỉnh....
Giải bài tập trang 54 bài ôn tập chương III Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu III.5: Cho tam giác ABC cân tại C. Kẻ các đường cao...
