Bài 1 trang 75 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Quan sát Hình 8. Tìm số thích hợp để ghi vào chỗ chấm trong các đẳng thức sau:

\(\begin{array}{l}EG = ...EM;\,\,\,GM = ...EM;\,\,\,\,GM = ...EG\\FG = ...GN;\,\,\,\,\,FN = ...GN;\,\,\,\,\,FN = ...FG\end{array}\)

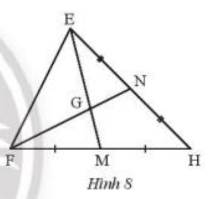
Lời giải: 

\(\begin{array}{l}EG = \dfrac{2}{3}EM;\,\,\,GM = \dfrac{1}{3}EM;\,\,\,\,GM = \dfrac{1}{2}EG\\FG = 2GN;\,\,\,\,\,FN = 3GN;\,\,\,\,\,\,\,FN = \dfrac{3}{2}FG\end{array}\)

Bài 2 trang 75 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

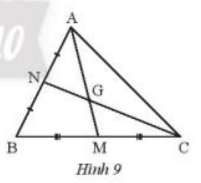
Quan sát Hình 9

a) Biết AM = 15 cm, tính AG

b) Biết GN = 6 cm, tính CN

Lời giải:

a) Theo đề bài ta có AM = 15 cm

Mà CN và AM là 2 trung tuyến của tam giác ABC

AM cắt CN tại G nên G là trọng tâm tam giác ABC

\( \Rightarrow AG = \dfrac{2}{3}AM\)(định lí về trọng tâm tam giác)

\( \Rightarrow AG = \dfrac{2}{3}\,15cm = 10cm\)

b) Vì G là trọng tâm tam giác ABC

\( \Rightarrow CG = \dfrac{2}{3}CN\)(theo tính chất của trung tuyến đi qua trọng tâm)

Mà \(CG + GN = CN\) nên ta có \(GN = CN - CG = CN - \dfrac{2}{3}CN = \dfrac{1}{3}CN\)

Theo giả thiết GN = 6cm ta có

\( \Rightarrow CN = 3GN = 3.6cm = 18cm\) 

Bài 3 trang 75 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG.

a) Chứng minh rằng BG song song với EC.

b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh rằng AF = 2FI

Lời giải:

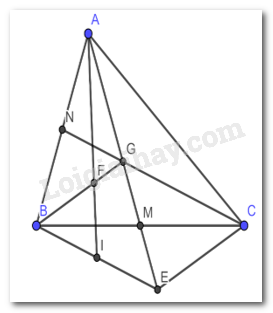
a) Xét tam giác BGM và tam giác CEM có :

\(\widehat {GMB} = \widehat {EMC}\)(2 góc đối đỉnh)

GM = ME (do G đối xứng E qua M)

MB = MC (do M là trung điểm của BC)

\( \Rightarrow \Delta BGM = \Delta CEM(c - g - c)\)

\( \Rightarrow \widehat {GBM} = \widehat {MCE}\)(2 góc tương ứng bằng nhau)

Mà 2 góc trên ở vị trí so le trong nên BG⫽CE

b) Vì I là trung điểm BE nên AI sẽ là trung tuyến của tam giác ABE

Và BG cũng là trung tuyến của tam giác ABE do G là trung điểm AE

Vì BG cắt AI tại F nên F sẽ là trọng tâm của tam giác ABE

\(\, \Rightarrow AF = \dfrac{2}{3}AI\)(định lí về trọng tâm tam giác)

Mà AI = AF + FI \( \Rightarrow \) FI = AI – AF

\( \Rightarrow FI = AI - \dfrac{2}{3}AI = \dfrac{1}{3}AI\)

\( \Rightarrow 2FI = AF = \dfrac{2}{3}AI\)

\( \Rightarrow \) AF = 2 FI

Bài 4 trang 75 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.

a) Chứng minh rằng BM = CN

b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC

Lời giải:

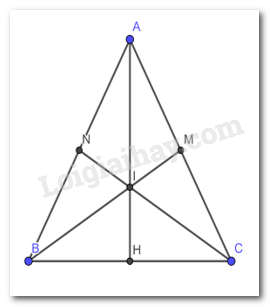
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.

Vì AB = AC (tính chất tam giác cân)

\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)

Xét tam giác AMB và tam giác ANC ta có :

AM = AN (cmt)

AB = AC

Góc A chung

\( \Rightarrow \Delta AMB =\Delta ANC\)

\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )

b) Vì BM và CN là các đường trung tuyến

Mà I là giao điểm của BM và CN

\( \Rightarrow \) I là trọng tâm của tam giác ABC

\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC

\( \Rightarrow \) H là trung điểm của BC

Bài 5 trang 76 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho tam giác ABC có đường trung tuyến BM bằng đường trung tuyến CN. Chứng minh rằng tam giác ABC cân.

Lời giải:

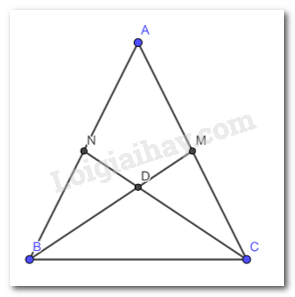
Gọi D là giao điểm của CN và BM

\( \Rightarrow \) D là trọng tâm tam giác ABC

\( \Rightarrow CD = \dfrac{2}{3}CN = BD = \dfrac{2}{3}BM\) ( do BM = CN )

\( \Rightarrow \) tam giác DBC cân tại D do BD = CD

\( \Rightarrow \) \(\widehat {DBC} = \widehat {DCB}\)(2 góc đáy trong tam giác cân)  (1)

Xét \(\Delta NDB\) và \(\Delta MDC\) có :

BD = CD

\(\widehat {NDB} = \widehat {MDC}\) (2 góc đối đỉnh)

ND = DM (do cùng \( = \dfrac{1}{3}CN = \dfrac{1}{3}BM\) (tính chất của trung trực đi qua trọng tâm tam giác ))

 \( \Rightarrow \Delta NDB=\Delta MDC\) (c.g.c)

\( \Rightarrow \,\widehat {NBD} = \widehat {MCD}\)(2 góc tương ứng) (2)

Từ (1) và (2) \( \Rightarrow \widehat {ABC} = \widehat {ACB}\) do \(\widehat {ABC} = \widehat {NBD} + \widehat {DBC}\) và \(\widehat {ACB} = \widehat {MCD} + \widehat {DCB}\)

\( \Rightarrow \Delta ABC\) cân tại A (do 2 góc bằng nhau)

Bài 6 trang 76 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF.

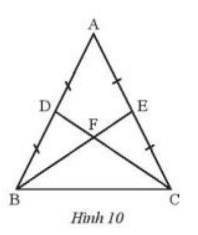
Lời giải: 

Vì BE, CD là 2 trung tuyến của tam giác ABC

NÊn E, D lần lượt là trung tuyến của AB và AC

\( \Rightarrow AD = AE = \dfrac{1}{2}AB = \dfrac{1}{2}AC\)

Xét tam giác ADC và tam giác AEB có :

AD = AE

Góc A chung

AB = AC (tam giác ABC cân tại A theo giả thiết)

\( \Rightarrow \Delta ADC = \Delta AEB(c - g - c)\)

\( \Rightarrow BE = CD\)(cạnh tương ứng)

Vì F là giao 2 trung tuyến nên F là trọng tâm tam giác ABC

\( \Rightarrow CF = BF = \dfrac{2}{3}BE = \dfrac{2}{3}CD\) ( định lí về trung tuyến đi qua trọng tâm tam giác )

\( \Rightarrow \dfrac{1}{3}BE = \dfrac{1}{3}CD \Rightarrow DF = FE = \dfrac{1}{3}.9cm = 3cm\)

\( \Rightarrow \) DF = 3 cm 

Giaibaitap.me