Câu 13 trang 138 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Trên hình bên có Ax song song với By, \(\widehat {{\rm{CAx}}} = 50^\circ ,\widehat {CBy} = 40^\circ \). Tính \(\widehat {ACB}\) bằng cách xem nó là góc ngoài của một tam giác.
Giải
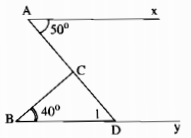
Kéo dài AC cắt By tại D.
Vì \(By{\rm{ }}//{\rm{ }}Ax{\rm{ }} = > \widehat {{D_1}} = \widehat A\) (2 góc so le trong)
Mà \(\widehat A = 50^\circ \left( {gt} \right)\) nên \(\widehat {{D_1}} = 50^\circ \)
Trong ∆DBC ta có \(\widehat {ACB}\) là góc ngoài tại đỉnh C
\( \Rightarrow \widehat {A{\rm{D}}C} = \widehat B + \widehat {{D_1}}\) (tính chất góc ngoài của tam giác)
\( \Rightarrow \widehat {A{\rm{D}}C} = 40^\circ + 50^\circ = 90^\circ \)
Câu 14 trang 138 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Chứng minh rằng tổng ba góc ngoài ở ba đỉnh của một tam giác thì bằng 360°.
Giải
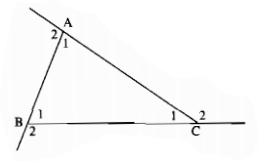
Ta có: \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (hai góc kề bù)
\(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) (hai góc kề bù)
\(\widehat {{C_1}} + \widehat {{C_2}} = 180^\circ \) (hai góc kề bù)
Suy ra: \(\widehat {{A_1}} + \widehat {{A_2}} + \widehat {{B_1}} + \widehat {{B_2}} + \widehat {{C_1}} + \widehat {{C_2}} = 180^\circ .3 = 540^\circ \)
\( \Rightarrow \widehat {{A_2}} + \widehat {{B_2}} + \widehat {{C_2}} = 540^\circ - \left( {\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}}} \right)\left( 1 \right)\)
Trong ∆ABC ta có:
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra:
$$\widehat {{A_2}} + \widehat {{B_2}} + \widehat {{C_2}} = 540^\circ - 180^\circ = 360^\circ $$
Câu 15 trang 138 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Cho tam giác ABC có \(\widehat A = 90^\circ \). Gọi E là một điểm nằm trong tam giác đó. Chứng minh rằng góc BEC là góc tù.
Giải
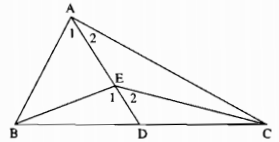
Kéo dài AE cắt BC tại D.
Trong ∆ABE ta có \(\widehat {{E_1}}\) là góc ngoài tại đỉnh E
Suy ra: \(\widehat {{E_1}} > \widehat {{A_1}}\) (tính chất góc ngoài của tam giác) (1)
Trong ∆AEC ta có \(\widehat {{E_2}}\) là góc ngoài tại đỉnh E
Suy ra: \(\widehat {{E_2}} > \widehat {{A_2}}\) (tính chất góc ngoài của tam giác) (2)
Cộng từng vế (1) và (2) ra có:
\(\widehat {{E_1}} + \widehat {{E_2}} > \widehat {{A_1}} + \widehat {{A_2}}\)
Hay \(\widehat {BEC} > \widehat {BAC} = 90^\circ \)
Vậy \(\widehat {BEC}\) là góc tù
Giaibaitap.me
Giải bài tập trang 139 bài 1 tổng ba góc của một tam giác Sách Bài Tập Toán lớp 7 tập 1. Câu 16: Cho tam giác ABC có...
Giải bài tập trang 139, 140 bài 2 hai tam giác bằng nhau Sách Bài Tập Toán lớp 7 tập 1. Câu 19: Hai tam giác trong hình dưới có bằng nhau hay không? Nếu có, hãy viết kí hiệu sự bằng nhau của hai tam giác đó....
Giải bài tập trang 140 bài 2 hai tam giác bằng nhau Sách Bài Tập Toán lớp 7 tập 1. Câu 23: Cho ∆ABC = ∆ DEF. Biết...
Giải bài tập trang 140, 141 bài 3 trường hợp bằng nhau thứ nhất của tam giác cạnh-cạnh-cạnh (c-c-c) Sách Bài Tập Toán lớp 7 tập 1. Câu 27: Vẽ tam giác ABC biết độ dài mỗi cạnh bằng 2,5cm. Sau đó đo mỗi góc của tam giác...
