Bài 9.31 trang 83 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.

Lời giải: 

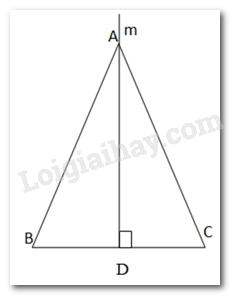
Từ A kẻ đường thẳng m vuông góc với BC tại trung điểm D của BC.

\( \Rightarrow \) AD là đường trung tuyến của BC.

Xét \(\Delta ABD\) và \(\Delta ACD\) có:

\(\begin{array}{l}\widehat {ADB} = \widehat {ADC} = {90^0}\\AD:chung\\BD = CD\left( {gt} \right)\\ \Rightarrow \Delta ABD = \Delta ACD\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow AB = AC\)(2 cạnh tương ứng)

\( \Rightarrow \Delta ABC\)cân tại A (đpcm). 

Bài 9.32 trang 83 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Cho ba điểm phân biệt thẳng hàng A, B, C. Gọi d là đường thẳng vuông góc với AB tại A. Với điểm M thuộc d, M khác A, vẽ đường thẳng CM. Qua B kẻ đường thẳng vuông góc với đường thẳng CM, cắt d tại N. Chứng minh đường thẳng BM vuông góc với đường thẳng CN.

Lời giải: 

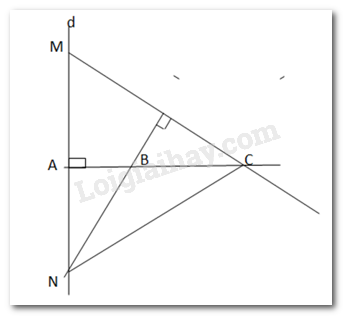
Xét tam giác MNC có

\(\begin{array}{l}BN \bot CM\\CA \bot MN\end{array}\)

\(BN \cap CA =\) {B}

\( \Rightarrow \) B là trực tâm của tam giác MNC

\( \Rightarrow MB \bot CN\)

Bài 9.33 trang 83 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Có một mảnh tôn hình tròn cần đục lỗ ở tâm. Làm thế nào để xác định được tâm của mảnh tôn đó?

Lời giải: 

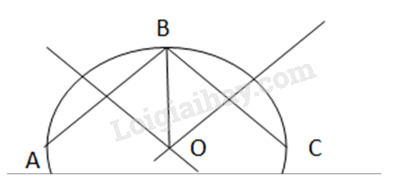
-Lấy ba điểm phân biệt A, B, C trên đường viền ngoài mảnh tôn.

- Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại O. Khi đó O là tâm cần xác định.

Bài 9.34 trang 83 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.

Lời giải: 

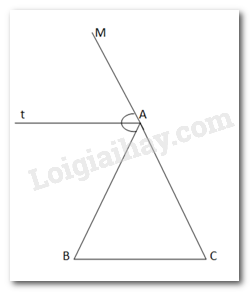
Gọi AM là tia đối của AC. At là đường phân giác của \(\widehat {MAB} \Rightarrow \widehat {MAt} = \widehat {BAt}\)

Ta có: \(At\parallel BC\) nên:

\(\widehat {ABC} = \widehat {BAt}\)(Hai góc sole trong)

\(\widehat {ACB} = \widehat {MAt}\)(Hai góc đồng vị)

Mà \(\widehat {MAt} = \widehat {BAt}\)\( \Rightarrow \widehat {ABC} = \widehat {ACB}\)

Vậy tam giác ABC cân tại A ( Dấu hiệu nhận biết tam giác cân).

Bài 9.35 trang 83 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Kí hiệu \({S_{ABC}}\) là diện tích tam giác ABC. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC.

a) Chúng minh \({S_{GBC}} = \dfrac{1}{3}{S_{ABC}}\)

Gợi ý: Sử dụng \(GM = \dfrac{1}{3}AM\) để chứng minh \({S_{GMB}} = \dfrac{1}{3}{S_{ABM}},{S_{GCM}} = \dfrac{1}{3}{S_{ACM}}\).

b) Chứng minh \({S_{GCA}} = {S_{GAB}} = \dfrac{1}{3}{S_{ABC}}\).

Lời giải: 

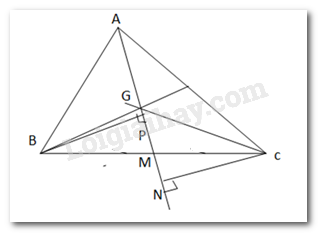
a)

Kẻ  \(BP \bot AM\), \(CN \bot AM\)

Sử dụng \(GM = \dfrac{1}{3}AM\) để chứng

minh \({S_{GMB}} = \dfrac{1}{3}{S_{ABM}},{S_{GCM}} = \dfrac{1}{3}{S_{ACM}}\).

b)

-Chứng minh \({S_{GAB}} = {S_{GAC}}\)

-Sử dụng \({S_{ABC}} = {S_{GAB}} + {S_{GAC}} + {S_{GBC}}\)

Giải

a) Vì G là trọng tâm tam giác ABC nên \(GM = \dfrac{1}{3}AM\)

Kẻ \(BP \bot AM\) ta có

 \(\begin{array}{l}{S_{GMP}} = \dfrac{1}{2}BP.GM\\{S_{ABM}} = \dfrac{1}{2}BP.AM\end{array}\)

\( \Rightarrow \dfrac{{{S_{GMP}}}}{{{S_{ABM}}}} = \dfrac{{GM}}{{AM}} = \dfrac{1}{3} \Rightarrow {S_{GMP}} = \dfrac{1}{3}{S_{ABM}}\)(1)                         

Tương tự, kẻ \(CN \bot AM\), ta có  

\(\begin{array}{l}{S_{GMC}} = \dfrac{1}{2}CN.GM\\{S_{ACM}} = \dfrac{1}{2}CN.AM\\ \Rightarrow \dfrac{{{S_{GMC}}}}{{{S_{ACM}}}} = \dfrac{{GM}}{{AM}} = \dfrac{1}{3} \Rightarrow {S_{GMC}} = \dfrac{1}{3}{S_{ACM}}\left( 2 \right)\end{array}\)

Cộng 2 vế của (1) và (2) ta có: 

\(\begin{array}{l}{S_{GMB}} + {S_{GMC}} = \dfrac{1}{3}\left( {{S_{AMC}} + {S_{ABM}}} \right)\\ \Rightarrow {S_{GBC}} = \dfrac{1}{3}{S_{ABC}}\end{array}\)

b) 

Ta có

\(\begin{array}{l}{S_{GAB}} = \dfrac{1}{2}BP.AG\\{S_{GAC}} = \dfrac{1}{2}CN.AG\end{array}\)

Xét \(\Delta BPM\) và \(\Delta CNM\) có:

\(\widehat {BPM} = \widehat {CNM} = {90^0}\)

 BM = CM ( M là trung điểm của BC)

\(\widehat {PMB} = \widehat {CMN}\)(2 góc đối đỉnh)

\( \Rightarrow \Delta BPM = \Delta CNM\)(cạnh huyền – góc nhọn)

\( \Rightarrow \) BP = CN (cạnh tương ứng)

\( \Rightarrow {S_{GAB}} = {S_{GAC}}\)

Ta có: \(AG = \dfrac{2}{3}AM\)

\(\begin{array}{l}{S_{ACB}} = {S_{GAB}} + {S_{GAC}} + {S_{GCB}}\\ \Rightarrow {S_{ACB}} = {S_{GAB}} + {S_{GAC}} + \dfrac{1}{3}{S_{ABC}}\\ \Rightarrow \dfrac{2}{3}{S_{ABC}} = 2{S_{GAC}}\\ \Rightarrow \dfrac{1}{3}{S_{ABC}} = {S_{GAC}} = {S_{GAB}}\end{array}\)

Giaibaitap.me