Câu 9.1 trang 51 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Hãy chọn khẳng định đúng trong các khẳng định sau:
(A) Trực tâm của một tam giác bao giờ cũng nằm trong tam giác.
(B) Trực tâm của một tam giác bao giờ cũng nằm ngoài tam giác.
(C) Trực tâm của một tam giác bao giờ cũng trùng với một đỉnh của tam giác.
(D) Cả ba khẳng định trên đều sai.
Giải
Trực tâm của tam giác nằm trong tam giác chỉ với tam giác nhọn, nằm ngoài tam giác chỉ với tam giác tù, trùng với một đỉnh của tam giác chỉ với tam giác vuông. Chọn (D) Cả ba khẳng định trên đều sai.
Câu 9.2 trang 52 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho tam giác ABC không là tam giác cân. Khi đó trực tâm của tam giác ABC là giao điểm của:
(A) Ba đường trung tuyến;
(B) Ba đường phân giác;
(C) Ba đường trung trực;
(D) Ba đường cao.
Hãy chọn phương án đúng.
Giải
Chọn (D) Ba đường cao.
Câu 9.3 trang 52 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho tam giác ABC có hai đường cao AH, BK cắt nhau tại điểm M. Hãy tính góc AMB biết  = 55°, \(\widehat B = 67^\circ \).
Giải
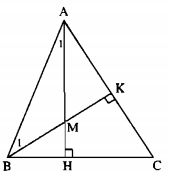
Để tính góc AMB, ta cần tính \(\widehat {{A_1}},\widehat {{B_1}}\)
Trong tam giác vuông AHB có \(\widehat {{A_1}} = 90^\circ - \widehat {ABH} = 90^\circ - 67^\circ = 23^\circ \)
Trong tam giác vuông AKB có \(\widehat {{B_1}} = 90^\circ - \widehat {BAK} = 90^\circ - 55^\circ = 35^\circ \)
Vậy trong tam giác AMB có
$$\widehat {AMB} = 180^\circ - \left( {\widehat {{A_1} + \widehat {{B_1}}}} \right) = 180^\circ - (23^\circ + 35^\circ ) = 122^\circ $$.
Giaibaitap.me
Giải bài tập trang 51 bài 9 tính chất ba đường cao của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 74: Cho tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của tam giác ABC, AHB, AHC....
Giải bài tập trang 51 bài 9 tính chất ba đường cao của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 78: Cho tam giác ABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC...
Giải bài tập trang 52 bài 9 tính chất ba đường cao của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 9.4: Cho tam giác nhọn ABC cân tại đỉnh A. Hai đường cao xuất phát từ đỉnh B và đỉnh C cắt nhau tại M...
Giải bài tập trang 52, 53 bài ôn tập chương III Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 82: Cho Tam giác ABC có AB < AC. Trên tia dối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA...
