Câu 89 trang 150 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây.

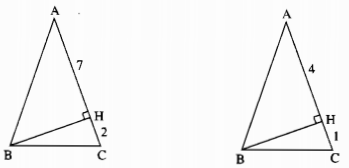
a) Trên hình bên trái: AH = 7cm, HC = 2cm

b) Trên hình bên phải: AH  = 4cm, HC = 1cm

Giải

a) ∆ABC cân tại A, ta có: AB = AC = 2 + 7 = 9

Trong tam giác vuông BHA, ta có \(\widehat {BHA} = 90^\circ \)

Áp dụng định lý Pytago, ta có: \(A{H^2} = B{H^2} + H{A^2}\)

Suy ra: \(B{H^2} = A{B^2} - A{H^2} = {9^2} - {7^2} = 81 - 49 = 32\)

Trong  tam giác vuông BHC, ta có \(\widehat {BHC} = 90^\circ \)

Áp dụng định lý Pytago, ta có:

\(B{C^2} = B{H^2} + H{C^2}\)

\(B{C^2} = 32 + {2^2} = 36 \Rightarrow BC = 6\)

b) ∆ABC cân tại A nên ta có: AB = AC = 4 +1 = 5

Trong tam giác vuông BHA, ta có: \(\widehat {BAH} = 90^\circ \)

Áp dụng định lý Pytago, ta có: \(A{B^2} = B{H^2} + H{A^2}\)

Suy ra: \(B{H^2} = A{B^2} - H{A^2} = {5^2} - {4^2} = 25 - 16 = 9\)

Trong tam giác vuông BHC, ta có \(\widehat {BHC} = 90^\circ \)

Áp dụng định lý Pytago, ta có:

\(B{C^2} = B{H^2} + H{C^2}\)

\(B{C^2} = 9 + {1^2} = 10 \Rightarrow BC = \sqrt {10} \)

Câu 90 trang 150 Sách Bài Tập (SBT) Toán lớp 7 tập 1

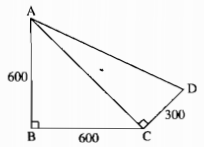
Bạn An đi từ nhà mình (A) qua nhà bạn Bảo (B) rồi đến nhà bạn Châu (C). Lúc về, An qua nhà bạn Dũng (D) rồi trở về nhà mình (hình bên). So sánh quãng đường lúc đi và quãng đường lúc về của An, quãng đường nào dài hơn.

Giải

Trong tam giác vuông ABC có \(\widehat {ABC} = 90^\circ \)

Áp dụng định lý Pytago, ta có: 

\(A{C^2} = A{B^2} + B{C^2} \)

          \(= {600^2} + {600^2} \)

          \(= 360000 + 360000 \)

          \(= 720000\)

Trong tam giác vuông ACD, ta có \(\widehat {AC{\rm{D}}} = 90^\circ \)

Áp dụng đinh lý Pytago, ta có: 

\(A{{\rm{D}}^2} = A{C^2} + C{{\rm{D}}^2} \)

          \(= 720000 + {300^2} \)

          \(= 720000 + 90000 \)

          \(= 810000\)

Suy ra: AD = 900m

Quãng đường ABC dài 600 + 600 = 1200 (m)

Quãng đường CDA dài 300 + 900 = 1200 (m)

Vậy quãng đường lúc đi và lúc về của An là bằng nhau.

Câu 91 trang 150 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho các số: 5; 8; 9; 12; 13; 15; 17

Hãy chọn ra các bộ ba có thể là độ dài ba cạnh của một tam giác vuông.

Giải

Ta có: \({5^2} = 25\)                      \({8^2} = 64\)

            \({9^2} = 81\)                      \({12^2} = 144\)

            \({13^2} = 169\)                 \({15^2} = 225\)

            \({17^2} = 289\)

Ta có:      25 + 144 = 169 hay \({5^2} + {12^2} = {13^2}\)

                 81 + 144 = 225 hay \({9^2} + {12^2} = {15^2}\)

Theo định lý đảo định lý Pytago thì bộ ba số 5;12;13 và 9;12;15 là độ dài 3 cạnh của một tam giác vuông.

Câu 92 trang 150 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình dưới) là tam giác vuông cân.

Giải

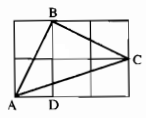
Đặt độ dài cạnh ô vuông là 1 (đơn vị chiều dài)

Áp dụng định lý Pytago ta có:

\(\eqalign{
& {\rm{A}}{B^2} = {1^2} + {2^2} = 1 + 4 = 5 \cr
& B{C^2} = {1^2} + {2^2} = 1 + 4 = 5 \cr
& A{C^2} = {3^2} + {1^2} = 9 + 1 = 10 \cr} \)

Suy ra: \({\rm{A}}{C^2} = A{B^2} + B{C^2}\)

Áp dụng định lý đảo định lý Pytago ta có ∆ABC vuông tại B.

Suy ra: \({\rm{A}}{C^2} = B{C^2} = 5\)

\( \Rightarrow \) AB = BC. Vậy ∆ABC vuông cân tại B.

Giaibaitap.me