Câu 93 trang 151 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Cho tam giác ABC cân tại A. Kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A.
Giải
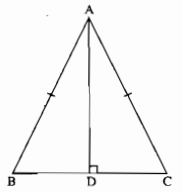
Xét tam giác vuông ADB và ADC, ta có:
\(\widehat {A{\rm{D}}B} = \widehat {A{\rm{D}}C} = 90^\circ \)
AB = AC (gt)
AD cạnh chung
Suy ra:
∆ADB = ∆ADC (cạnh huyền, cạnh góc vuông)
\( \Rightarrow \widehat {BA{\rm{D}}} = \widehat {CA{\rm{D}}}\) (hai góc tương ứng)
Vậy AD là tia phân giác \(\Rightarrow \widehat {BA{\rm{D}}} = \widehat {CA{\rm{D}}}\)
Câu 94 trang 151 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Cho tam giác ABC cân tại A. Kẻ BD vuông góc với AC, kẻ CE vuông góc với AB. Gọi K là giao điểm của BD và CE. Chứng minh rằng AK là tia phân giác của góc A.
Giải
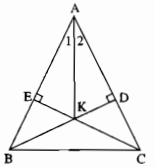
Xét hai tam giác vuông ADB và AEC, ta có:
\(\widehat {A{\rm{D}}B} = \widehat {A{\rm{E}}C} = 90^\circ \)
AB = AC (gt)
\(\widehat {DAB} = \widehat {E{\rm{A}}C}\)
\( \Rightarrow \) ∆ADB = ∆AEC (cạnh huyền, góc nhọn)
Suy ra: AD = AE (hai cạnh tương ứng)
Xét hai tam giác vuông ADK và AEK, ta có:
\(\widehat {A{\rm{D}}K} = \widehat {A{\rm{E}}K} = 90^\circ \)
AD = AE (chứng minh trên)
AK cạnh chung
Suy ra: ∆ADK = ∆AEK (cạnh huyền, cạnh góc vuông)
Suy ra: \(\widehat {DAK} = \widehat {E{\rm{A}}K}\) (2 góc tương ứng)
Vậy AK là tia phân giác của góc BAC.
Câu 95 trang 151 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Tam giác ABC có M là trung điểm của BC, AM là tia phân giác của góc A. Kẻ MH vuông góc với AB, MK vuông góc với AC. Chứng minh rằng:
a) MH = MK
b) \(\widehat B = \widehat C\)
Giải
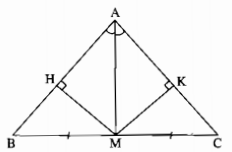
a) Xét hai tam giác vuông AHM và AKM, ta có:
\(\widehat {AHM} = \widehat {AKM} = 90^\circ \)
Cạnh huyền AM chung
\(\widehat {HAM} = \widehat {K{\rm{A}}M}\) (gt)
\( \Rightarrow \) ∆AHM = ∆AKM (cạnh huyền, góc nhọn)
Suy ra: MH = MK (hai cạnh tương ứng)
b) Xét hai tam giác vuông MHB và MKC, ta có:
\(\widehat {MHB} = \widehat {MKC} = 90^\circ \)
MH = MK (chứng minh trên)
MC = MB (gt)
Suy ra: ∆MHB = ∆MKC (cạnh huyền, cạnh góc vuông)
Suy ra: \(\widehat B = \widehat C\) (hai góc tương ứng)
Giaibaitap.me
Giải bài tập trang 151 bài 8 các trường hợp bằng nhau của tam giác vuông Sách Bài Tập Toán lớp 7 tập 1. Câu 99: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. ..
Giải bài tập trang 151 bài 8 các trường hợp bằng nhau của tam giác vuông Sách Bài Tập Toán lớp 7 tập 1. Câu 96: Cho tam giác ABC cân tại A. Các đường trung trực của AB, AC cắt nhau ở I. Chứng minh rằng AI là tia phân giác của góc A...
Giải bài tập trang 152, 153 bài ôn tập chương II Tam giác Sách Bài Tập Toán lớp 7 tập 1. Câu 103: Cho đoạn thẳng AB. Vẽ các cung tâm A và B có cùng bán kính sao cho chúng cắt nhau tại C và D...
Giải bài tập trang 152 bài 9 thực hành ngoài trời Sách Bài Tập (SBT) Toán lớp 7 tập 1. Câu 102: Dựa vào hình bên hãy nêu cách xác định khoảng cách giữa hai điểm A, B bị ngăn bởi con sông....
