Bài 7.12 trang 33 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Tìm tổng của hai đa thức sau bằng cách nhóm các hạng tử cùng bậc:

x² – 3x + 2 và 4x³ – x² + x - 1

Lời giải: 

Ta có: (x² – 3x + 2) + (4x³ – x² + x – 1)

=  x² – 3x + 2 + 4x³ – x² + x - 1

= 4x³ + (x² – x² ) + (-3x + x) + (2 – 1)

 = 4x³ – 2x + 1

Bài 7.13 trang 33 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Tìm hiệu sau theo cách đặt tính trừ: (- x³ – 5x + 2) – (3x + 8)

Lời giải: 

Đặt phép tính ta được:

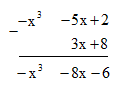
Vậy (- x³ – 5x + 2) – (3x + 8) = -x³ - 8x - 6.

Bài 7.14 trang 33 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Cho hai đa thức:

\(A = 6{x^4} - 4{x^3} + x - \dfrac{1}{3};B =  - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3}\)

Tính A + B và A - B

Lời giải: 

\(\begin{array}{l}A + B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) + ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3}\\ = (6{x^4} - 3{x^4}) + ( - 4{x^3} - 2{x^3}) - 5{x^2} + (x + x) + ( - \dfrac{1}{3} + \dfrac{2}{3})\\ = 3{x^4} - 6{x^3} - 5{x^2} + 2x + \dfrac{1}{3}\\A - B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) - ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} + 3{x^4} + 2{x^3} + 5{x^2} - x - \dfrac{2}{3}\\ = (6{x^4} + 3{x^4}) + ( - 4{x^3} + 2{x^3}) + 5{x^2} + (x - x) + ( - \dfrac{1}{3} - \dfrac{2}{3})\\ = 9{x^4} - 2{x^3} + 5{x^2} - 1\end{array}\)\(\begin{array}{l}A + B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) + ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3}\\ = (6{x^4} - 3{x^4}) + ( - 4{x^3} - 2{x^3}) - 5{x^2} + (x + x) + ( - \dfrac{1}{3} + \dfrac{2}{3})\\ = 3{x^4} - 6{x^3} - 5{x^2} + 2x + \dfrac{1}{3}\\A - B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) - ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} + 3{x^4} + 2{x^3} + 5{x^2} - x - \dfrac{2}{3}\\ = (6{x^4} + 3{x^4}) + ( - 4{x^3} + 2{x^3}) + 5{x^2} + (x - x) + ( - \dfrac{1}{3} - \dfrac{2}{3})\\ = 9{x^4} - 2{x^3} + 5{x^2} - 1\end{array}\)

Bài 7.15 trang 33 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Cho các đa thức:

\(A = 3{x^4} - 2{x^3} - x + 1;B =  - 2{x^3} + 4{x^2} + 5x;C =  - 3{x^4} + 2{x^2} + 5\)

Tính A + B + C; A – B + C  và A – B – C

Lời giải: 

\(\begin{array}{l}A + B + C = (3{x^4} - 2{x^3} - x + 1) + ( - 2{x^3} + 4{x^2} + 5x) + ( - 3{x^4} + 2{x^2} + 5)\\ = 3{x^4} - 2{x^3} - x + 1 - 2{x^3} + 4{x^2} + 5x - 3{x^4} + 2{x^2} + 5\\ = (3{x^4} - 3{x^4}) + ( - 2{x^3} - 2{x^3}) + (4{x^2} + 2{x^2}) + ( - x + 5x) + (1 + 5)\\ = 0 + ( - 4{x^3}) + 6{x^2} + 4x + 6\\ =  - 4{x^3} + 6{x^2} + 4x + 6\\A - B + C = (3{x^4} - 2{x^3} - x + 1) - ( - 2{x^3} + 4{x^2} + 5x) + ( - 3{x^4} + 2{x^2} + 5)\\ = 3{x^4} - 2{x^3} - x + 1 + 2{x^3} - 4{x^2} - 5x - 3{x^4} + 2{x^2} + 5\\ = (3{x^4} - 3{x^4}) + ( - 2{x^3} + 2{x^3}) + ( - 4{x^2} + 2{x^2}) + ( - x - 5x) + (1 + 5)\\ = 0 + 0 + ( - 2{x^2}) - 6x + 6\\ =  - 2{x^2} - 6x + 6\\A - B - C = (3{x^4} - 2{x^3} - x + 1) - ( - 2{x^3} + 4{x^2} + 5x) - ( - 3{x^4} + 2{x^2} + 5)\\ = 3{x^4} - 2{x^3} - x + 1 + 2{x^3} - 4{x^2} - 5x + 3{x^4} - 2{x^2} - 5\\ = (3{x^4} + 3{x^4}) + ( - 2{x^3} + 2{x^3}) + ( - 4{x^2} - 2{x^2}) + ( - x - 5x) + (1 - 5)\\ = 6{x^4} + 0 + ( - 6{x^2}) - 6x + ( - 4)\\ = 6{x^4} - 6{x^2} - 6x - 4\end{array}\)

Bài 7.16 trang 33 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Bạn Nam được phân công mua một số sách làm quà tặng trong buổi tổng kết cuối năm học của lớp. Nam dự định mau ba loại sách với giá bán như bảng sau. Giả sử Nam cần mua x cuốn sách khoa học, x+8 cuốn sách tham khảo và x + 5 cuốn truyện tranh.

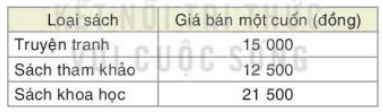
a) Viết các đa thức biểu thị số tiền Nam phải trả cho từng loại sách.

b) Tìm đa thức biểu thị tổng số tiền Nam phải trả để mua số sách đó.

Lời giải: 

a) Đa thức biểu thị số tiền Nam phải trả cho truyện tranh là: A = (x +5). 15 000 = 15 000x + 75 000 ( đồng)

Đa thức biểu thị số tiền Nam phải trả cho sách tham khảo là: B = (x + 8) . 12 500 = 12 500x + 100 000 ( đồng)

Đa thức biểu thị số tiền Nam phải trả cho sách khoa học là: C = x . 21 500 (đồng)

b) Đa thức biểu thị tổng số tiền Nam phải trả để mua số sách đó là:

P = A + B + C = = 15 000x + 75 000  + 12 500x + 100 000 + x . 21 500

= (15 000 + 12 500 + 21 500)x + (75 000 + 100 000)

= 49 000x + 175 000 ( đồng)

Bài 7.17 trang 33 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Trên một mảnh đất hình chữ nhật có chiều dài 65 m, người ta định làm một bể bơi có chiều rộng là x nét, chiều dài gấp 3 lần chiều rộng. Sơ đồ và kích thước cụ thể (tính bằng mét) đươc cho trong Hình 7.1. Tìm đa thức ( biến x):

a) Biểu thị diện tích bể bơi

b) Biểu thị diện tích mảnh đất

c) Biểu thị diện tích phần đất xung quanh bể bơi.

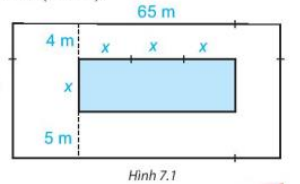
Lời giải: 

a) Bể bơi có chiều dài là 3x, chiều rộng là x nên đa thức biểu thị diện tích bể bơi là:

B = 3x. x = 3.x²

b) Mảnh đất có chiều dài là 65, chiều rộng là 5 + x + 4 = x + 9 nên đa thức biểu thị diện tích mảnh đất là:

D = 65. (x+9) = 65x + 585

c) Diện tích xung quanh bể bơi  = diện tích mảnh đất – diện tích bể bơi nên đa thức biểu thị diện tích phần đất xung quanh bể bơi là:

Q = D – B = 65x + 585 - 3.x² = -3.x² +65x + 585

Giaibaitap.me