Bài 9.26 trang 81 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB.

Lời giải: 

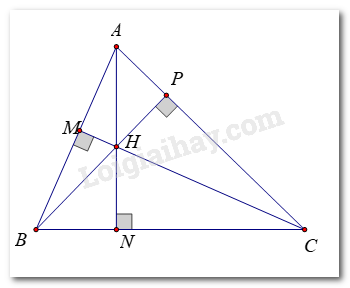
a)

Trong ΔABC ta có H là trực tâm nên:

AH ⊥ BC tại N, BH ⊥ AC tại P, CH ⊥ AB tại M

Trong ΔAHB, ta có:

       HM ⊥ AB

       BN ⊥ AH

Mà MH cắt BN tại C

=> C là trực tâm của tam giác AHB.

Trong ΔHAC, ta có:

       HP ⊥ AC

       CN ⊥ AH

Mà HP cắt CN tại B

=> B là trực tâm của ΔHAC.

Trong ΔHBC, ta có:

       HN ⊥ BC

       BM ⊥ HC

Mà HN cắt BM tại A

=> A là trực tâm của tam giác HBC

Bài 9.27 trang 81 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Cho tam giác ABC có \(\widehat A = {100^0}\)  và trực tâm H. Tìm góc BHC.

Lời giải: 

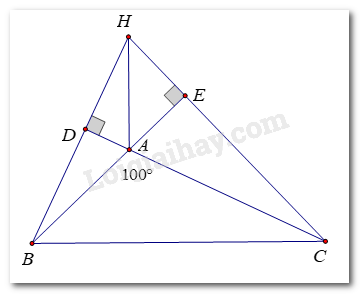
Gọi E là chân đường cao từ C xuống AB, D là chân đường cao từ B xuống AC

=> HC ⊥ BE, HB ⊥ CD

Ta có:

\(\begin{array}{l}\widehat {BAC} + \widehat {BAD} = {180^0}\\ \Rightarrow {100^0} + \widehat {BAD} = {180^0}\\ \Rightarrow \widehat {BAD} = {180^0} - {100^0}\\ \Rightarrow \widehat {BAD} = {80^0}\end{array}\)

∆ ADB là tam giác vuông tại D:

\(\begin{array}{l}\widehat {BAD} + \widehat {ABD} = {90^0}\\ \Rightarrow {80^0} + \widehat {ABD} = {90^0}\\ \Rightarrow \widehat {ABD} = {10^0}\end{array}\)

∆ BEH là tam giác vuông tại E

\(\begin{array}{l}\widehat {EBH} + \widehat {BHE} = {90^0}\\ \Rightarrow {10^0} + \widehat {BHE} = {90^0}\\ \Rightarrow \widehat {BHE} = {80^0}\end{array}\)

Hay \(\widehat {BHC} = {80^0}\) 

Bài 9.28 trang 81 sách giáo khoa Toán 7 Kết nối tri thức tập 2

Xét điểm O cách đều 3 đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.

Lời giải: 

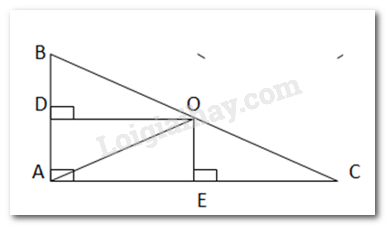
O cách đều 3 đỉnh của tam giác ABC

\( \Rightarrow \) \(OA = OB = OC\)

\( \Rightarrow \) \(\Delta OAB\) cân tại O.

Giả sử O là trung điểm BC

\( \Rightarrow \widehat {OAB} = \widehat {OBA}\)

 \(\Delta OAC\) cân tại O 

\( \Rightarrow \widehat {OAC} = \widehat {OCA}\)

Xét tam giác ABC có

\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\ \Rightarrow \widehat A + \widehat {OAB} + \widehat {OAC} = {180^0}\\ \Rightarrow \widehat A + \widehat A = {180^0}\\ \Rightarrow \widehat A = {90^0}\end{array}\)

Vậy nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.

Bài 9.29 trang 81 sách giáo khoa Toán 7 Kết nối tri thức tập 2

a) Có một chi tiết máy ( đường viền ngoài là đường tròn) bị gãy. (H.9.46). Làm thế nào để xác định được bán kính của đường viền này ?

b) Trên bản đồ, ba khu dân cư được quy hoạch tại điểm A, B, C không thẳng hàng. Hãy tìm trên bản đồ một điểm M cách đều A, B, C để quy hoạch một trường học

Lời giải: 

a)

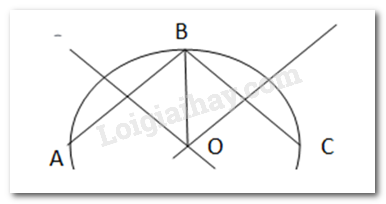
- Lấy ba điểm phân biệt A, B, C trên đường viền ngoài chi tiết máy.

- Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại O. Khi đó O là tâm cần xác định.

- Bán kính đường tròn cần tìm là độ dài đoạn OB (hoặc OA hoặc OC).

b)

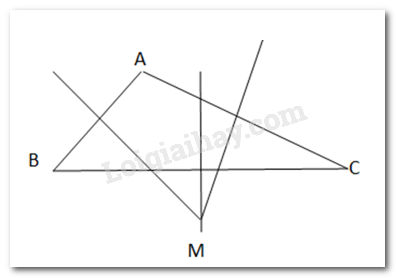
- Bước 1: Vẽ đường trung trực của các đoạn AB, AC, BC

- Bước 2: 3 đường trung trực này cắt nhau tại M. Khi đó MA= MB=MC.

- Bước 3: M là điểm cần xác định.

Bài 9.30 trang 81 sách giáo khoa Toán 7 Kết nối tri thức tập 2

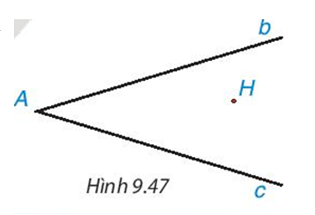
Cho hai đường thẳng không vuông góc b,c cắt nhau tại điểm A và cho điểm H không thuộc b và c (H.9.47). Hãy tìm điểm B thuộc b, điểm C thuộc c sao cho tam giác ABC nhận H làm trực tâm.

Lời giải: 

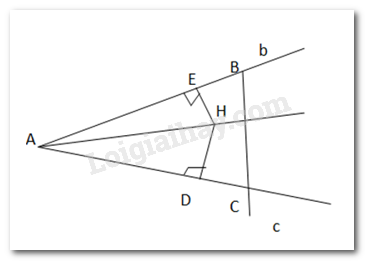
- Kẻ HD \( \bot \) đường thẳng c tại điểm D, HE \( \bot \) đường thẳng b tại điểm E

- Nối A với H. Kéo dài DH cắt đường thẳng b tại B.

Từ B kẻ đường vuông góc với AH, đường thẳng đó cắt đường thẳng c tại 1 điểm. Điểm đó chính là điểm C.

=> H là trực tâm của tam giác ABC. 

Giaibaitap.me