Bài 1 trang 62 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

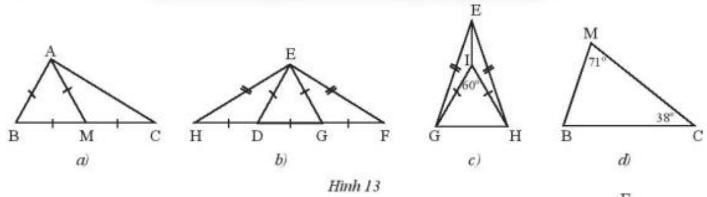
Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích.

Lời giải: 

a) Tam giác ABM là tam giác đều do có 3 cạnh bằng nhau

   Tam giác AMC cân tại M do AM = MC

b) Tam giác EDG là tam giác đều do có 3 cạnh bằng nhau

   Tam giác EHF cân tại E do EH = EF

   Tam giác EDH cân tại D do DH = DE

c) Tam giác EGF cân tại G do GE = GF

   Tam giác IHG đều do là tam giác cân có 1 góc = 60°

   Tam giác EHG cân tại E do EG = EH

d) Tam giác MBC không cân và không đều vì 3 góc có số đo khác nhau

Bài 2 trang 62 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

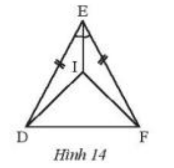
Cho Hình 14, biết ED = EF và EI là tia phân giác của \(\widehat {DEF}\)

Chứng minh rằng:

a) \(\Delta EID = \Delta EIF\)

b) Tam giác DIF cân

Lời giải: 

a) Xét tam giác EID và tam giác EIF có :

IE chung

ED = EF

\(\widehat {IED} = \widehat {IEF}\)( EI là tia phân giác của \(\widehat {DEF}\))

\( \Rightarrow \Delta EID = \Delta EIF(c - g - c)\)

b) Vì \(\Delta EID = \Delta EIF\) nên ID = IF ( 2 cạnh tương ứng )

Do đó tam giác DIF cân tại I (theo định nghĩa tam giác cân)

Bài 3 trang 63 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

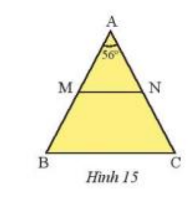
Cho tam giác ABC cân tại A có \(\widehat A = {56^o}\)(Hình 15)

a) Tính\(\widehat B\), \(\widehat C\)

b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.

c) Chứng minh rằng MN // BC

Lời giải:

a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\)

Mà \( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)

\( \Rightarrow \widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\)

b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )

Mà M, N là trung điểm của AB, AC

Nên AM = AN

Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A

\( \Rightarrow \widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\)

c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°)

Mà chúng ở vị trí đồng vị nên MN⫽BC

Bài 4 trang 63 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E.

a) Chứng minh rẳng \(\widehat {ABF} = \widehat {ACE}\)

b) Chứng minh rằng tam giác AEF cân

c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và tam giác IEF là những tam giác cân

Lời giải:

a) Vì tam giác ABC cân tại A

\( \Rightarrow \widehat B = \widehat C \Rightarrow \dfrac{1}{2}\widehat B = \dfrac{1}{2}\widehat C \Rightarrow \widehat {ABF} = \widehat {ACE}\)

b) Xét \(\Delta ECA\) và \(\Delta FBA\)có:

\(\widehat{A}\) chung

AB = AC

\(\widehat {ABF} = \widehat {ACE}\)

\( \Rightarrow \)\(\Delta ECA\)= \(\Delta FBA\)( g – c – g )

\( \Rightarrow AE = AF và EC = BF\) (2 cạnh tương ứng)

\( \Rightarrow \Delta AEF\) cân tại A

c) Xét tam giác IBC có :

\(\widehat B = \widehat C \Rightarrow \dfrac{1}{2}\widehat B = \dfrac{1}{2}\widehat C \Rightarrow \widehat {ICB} = \widehat {IBC}\)

Do đó, tam giác IBC cân tại I ( 2 góc ở đáy bằng nhau )

\( \Rightarrow IB = IC\)( cạnh tương ứng )

Vì EC = BF ( câu b) và IB = IC

\( \Rightarrow \) EC – IC = BF – BI

\( \Rightarrow \) EI = FI

\( \Rightarrow \Delta IEF\) cân tại I

Bài 5 trang 63 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

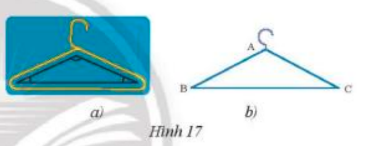
Phần thân của một móc treo quần áo có dạng hình tam giác cân (Hình 17a) được vẽ lại như Hình 17b. Cho biết AB = 20 cm; BC = 28 cm và \(\widehat B\)= 35°. Tìm số đo các góc còn lại và chu vi của tam giác ABC.

Lời giải:

Vì tam giác ABC cân tại A

\( \Rightarrow \) AB = AC ( định lí tam giác cân ) = 20 cm

\( \Rightarrow \) Chu vi tam giác ABC = AB + AC + BC = 20 + 20 + 28 = 68 cm

Vì ABC là tam giác cân tại A \( \Rightarrow \widehat B = \widehat C\) ( 2 góc ở đáy ) = 35°

Mà theo định lí tổng 3 góc trong tam giác = 180°

\( \Rightarrow \widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {35^o} - {35^o} = {110^o}\)

Bài 6 trang 63 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.

a) Cho biết \(\widehat {{A_1}}\)\( = {42^o}\). Tính số đo của \(\widehat {{M_1}}\),\(\widehat {{B_1}}\),\(\widehat {{M_2}}\).

b) Chứng minh MN // BC, MP // AC.

c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.

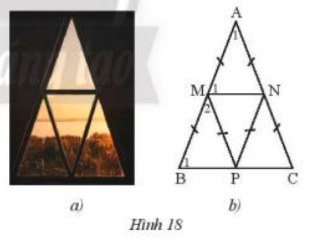
Lời giải:

a)      Ta thấy tam giác AMN cân tại A do AM = AN

\( \Rightarrow \widehat {{M_1}} = ({180^o} - \widehat {{A_1}}):2 = ({180^o} - {42^o}):2 = {69^o}\)

Ta thấy tam giác PMN = tam giác AMN ( c-c-c )

\( \Rightarrow \widehat {{M_1}} = \widehat {PMN} = {69^o}\) (góc tương ứng )

Mà \( \Rightarrow \widehat {{M_1}} + \widehat {{M_2}} + \widehat {PMN} = {180^o}\)( các góc kề bù )

\( \Rightarrow \widehat {{M_2}} = {180^o} - {69^o} - {69^o} = {42^o}\)

Mà tam giác MPB cân tại M do MB = MP nên

\( \Rightarrow \widehat {{B_1}} = \widehat {MPB}\)

Áp dụng định lí tổng 3 góc trong tam giác

\( \Rightarrow \widehat {{B_1}} = ({180^o} - {42^o}):2 = {69^o}\)

b)      Ta thấy \(\widehat {{B_1}}\)và \(\widehat {{M_1}}\)ở vị trí đồng vị và bằng nhau nên

\( \Rightarrow \)MN⫽BC

Vì tam giác PMN = tam giác AMN nên ta có

\( \Rightarrow \widehat {{M_1}} = \widehat {ANM} = \widehat {PMN} = \widehat {MNP}\)( do 2 tam giác cân và bằng nhau )

Mà \(\widehat {MNA}\)và\(\widehat {PMN}\) ở vị trí so le trong

\( \Rightarrow \)MP⫽AC

c)      Ta có \(\Delta AMN = \Delta PMN = \Delta MBP(c - g - c)\)(1)

Vì MP⫽AC ( chứng minh trên )

\( \Rightarrow \widehat {MPN} = \widehat {PNC}\) ( 2 góc so le trong ) =\({42^o}\)

\( \Rightarrow \Delta MPN = \Delta NCP(c - g - c)\)(2)

Từ (1) và (2) \( \Rightarrow \) 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau 

Giaibaitap.me