Bài 1 trang 57 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Quan sát Hình 23 rồi thay dấu ? bằng tên tam giác thích hợp.

a) $△$ABE = $△$?

b) $△$EAB = $△$?

c) $△$? = $△$CDE. 

Lời giải: 

Quan sát Hình 23 ta thấy:

a) Xét ∆ABE và ∆DCE có:

AB = DC (theo giả thiết).

BE = CE (theo giả thiết).

AE = DE (theo giả thiết).

Suy ra ∆ABE = ∆DCE (c.c.c).

Vậy ∆ABE = ∆DCE.

b) Do ∆ABE = ∆DCE (chứng minh trên) nên ∆EAB = ∆EDC.

c) Do ∆ABE = ∆DCE (chứng minh trên) nên ∆BAE = ∆CDE.

Bài 2 trang 57 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho \(\Delta{DEF}=\Delta{HIK}\) và \(\widehat D= {73^o}\), DE = 5cm, IK = 7cm. Tính số đo \(\widehat H\) và độ dài HI, EF.

Lời giải: 

Vì \(\Delta{DEF}=\Delta{HIK}\)

\( \Rightarrow \widehat D = \widehat H\)( 2 góc tương ứng )

Mà \(\widehat D =73^0\)

\( \Rightarrow \widehat H=73^0\)

Vì \(\Delta{DEF}=\Delta{HIK}\)

 \(\Rightarrow DE = HI;EF = IK;DF = HK\)( các cạnh tương ứng )

Vậy \( \widehat H = {73^o};HI = 5cm;EF = 7cm\)

Bài 3 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho hai tam giác bằng nhau ABC và DEF (các đỉnh chưa viết tương ứng), trong đó \(\widehat A = \widehat E\), \(\widehat C = \widehat D\). Tìm các cặp cạnh bằng nhau, cặp góc tương ứng bằng nhau còn lại.

Lời giải: 

Vì \(\widehat A = \widehat E\), \(\widehat C = \widehat D\) nên đỉnh A tương ứng với đỉnh E, đỉnh C tương ứng với đỉnh D. 

\( \Rightarrow \widehat B = \widehat F\) ( 2 góc tương ứng)

Do đó, \(\Delta{ABC}=\Delta{EFD}\)

\(\Rightarrow AB = DE;BC = EF;AC = DF\)( các cạnh tương ứng )

Bài 4 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho biết \(\Delta{MNP}=\Delta{DEF}\) và MN = 4cm, MP = 5cm, EF = 6cm. Tính chu vi tam giác MNP.

Lời giải: 

Vì \(\Delta{MNP}=\Delta{DEF}\) 

\( \Rightarrow DE = MN;EF = NP;DF = MP\) (các cạnh tương ứng)

\( \Rightarrow NP = 6cm\)

\( \Rightarrow \) Chu vi tam giác MNP là:

C = MN + MP + NP = 4 + 5 + 6 = 15 (cm)

Bài 5 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

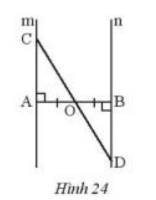
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm CD.

Lời giải: 

Xét \(\Delta OAC\) và \(\Delta OBD\), ta có:

\(\widehat {COA} = \widehat {BOD}\) ( 2 góc đối đỉnh)

AO = BO

\(\widehat A = \widehat B\)

\(\Rightarrow \Delta OAC=\Delta OBD\) ( g-c-g )

\( \Rightarrow CO = DO\) ( cạnh tương ứng )

\( \Rightarrow \) O là trung điểm CD

Bài 6 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

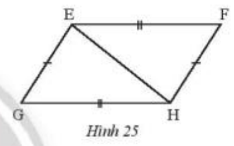
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:

a) \(\Delta EFH=\Delta HGE\)

b) EF // HG

Lời giải: 

a) Xét tam giác EGH và tam giác HFE có :

FE = GH; GE = HF; EH chung

\(\Rightarrow \Delta EFH=\Delta HGE\) (c-c-c)

\( \Rightarrow \widehat {FEH} = \widehat {EHG}\)( 2 góc tương ứng )

b) Vì \(\widehat {FEH}=\widehat {EHG}\)

Mà 2 góc này ở vị trí so le trong

Do đó, EF // HG

Bài 7 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho tam giác FGH có FG = FH. Lấy điểm I trên cạnh GH sao cho FI là tia phân giác của \(\widehat {GFH}\).Chứng minh rằng hai tam giác FIG và FIH bằng nhau.

Lời giải: 

Xét tam giác FIG và FIH có :

FI chung

FG = FH ( theo giả thiết )

\(\widehat {GFI} = \widehat {HFI}\) ( do FI là phân giác \(\widehat {GFH}\))

\(\Rightarrow \Delta FIG=\Delta FIH\) (c-g-c)

Bài 8 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:

a) AD = BC

b) \(\Delta EAB=\Delta ECD\)

c) OE là tia phân giác của góc xOy.

Lời giải: 

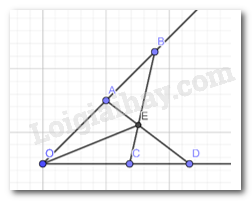
a) Xét \(\Delta OAD\) và \(\Delta OCB\), ta có :

OD = OB

\(\widehat{A}\) chung

OA = OC 

\(\Rightarrow \Delta OAD=\Delta OCB\) (c-g-c )

\( \Rightarrow AD = BC\)(2 cạnh tương ứng )

b) Vì \(\Delta OAD=\Delta OCB\) nên \(\widehat{OAD}=\widehat{OCB}; \widehat{D}=\widehat{B}\) ( 2 góc tương ứng)

Mà \(\widehat{OAD}+\widehat{BAD}=180^0\) ( 2 góc kề bù)

\(\widehat{OCB}+\widehat{BCD}=180^0\) ( 2 góc kề bù)

Do đó, \(\widehat{BAD}=\widehat{BCD}\)

Vì \(OA+AB=OB; OC+CD=OD\)

Mà \(OC = OA, OD = OB\)

\(\Rightarrow AB=CD\)

Xét \(\Delta EAB\) và \(\Delta ECD\), ta có:

\(\widehat {ABE} = \widehat {CDE}\)

\(AB = CD\)

\(\widehat {BAE} = \widehat {DCE}\)

\(\Rightarrow \Delta EAB=\Delta ECD\) (g-c-g)

c) Vì \(\Delta EAB=\Delta ECD\) nên EB = ED ( 2 cạnh tương ứng)

Xét \(\Delta OBE\) và \(\Delta ODE\), ta có :

 EB = ED

OB = OD

OE chung

\( \Rightarrow \Delta OBE=\Delta ODE \)  (c.c.c)

\( \Rightarrow \widehat{BOE}=\widehat{DOE}\) ( 2 góc tương ứng)

\( \Rightarrow \) OE là phân giác \(\widehat {xOy}\)

Bài 9 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

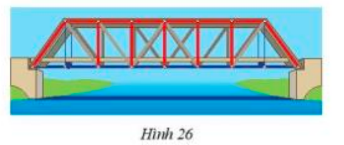
Đặt tên cho một số điểm có trong Hình 26 và chỉ ra ba cặp tam giác bằng nhau trong hình đó.

Lời giải: 

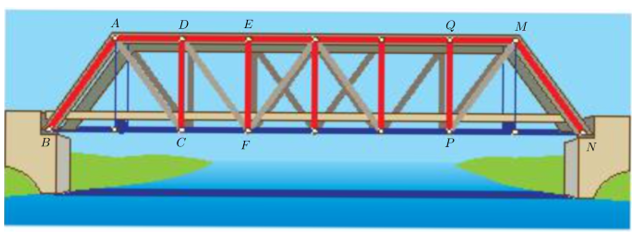
Đặt tên các điểm như hình trên.

Dựa vào hình trên ta có các cặp tam giác bằng nhau như sau:

∆ABC = ∆MNP; ∆ADC = ∆MQP; ∆ADC = ∆DEF.

Giaibaitap.me