Câu 42 trang 112 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Điền vào chỗ (…) để chứng minh bài toán sau:
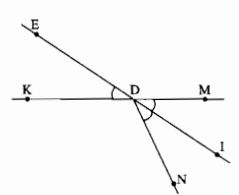
Gọi DI là tia phân giác của góc MDN. Gọi EDK là góc đối đỉnh của góc IDM. Chứng minh rằng \(\widehat {E{\rm{D}}K} = \widehat {I{\rm{D}}N}\).

Chứng minh:
\(\widehat {I{\rm{D}}M} = \widehat {I{\rm{D}}N}\) (Vì …) (1)
\(\widehat {I{\rm{D}}M} = \widehat {E{\rm{D}}K}\) (Vì …) (2)
Từ (1) và (2) suy ra ………
Đó là điều phải chứng minh.
Giải

Ta có: Chứng minh:
\(\widehat {I{\rm{D}}M} = \widehat {I{\rm{D}}N}\) (Vì DI là tia phân giác của \(\widehat {MDN}\)) (1)
\(\widehat {I{\rm{D}}M} = \widehat {E{\rm{D}}K}\) (Vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra: \(\widehat {E{\rm{D}}K} = \widehat {I{\rm{D}}N}\) (điều phải chứng minh)
Câu 43 trang 112 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Hãy chứng minh định lí:
Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.
Hướng dẫn: Chứng minh tương tự bài tập 30
Giải


Chứng minh:
Giả sử \(\widehat {{A_1}} \ne \widehat {{B_1}}\).
Qua B kẻ đường thẳng xy tạo với đường thẳng c có \(\widehat {ABy} = \widehat {{A_1}}\).
Theo dấu hiệu của hai đường thẳng song song, ta có xy // a.
Vì xy và a tạo ra với đường thẳng c cắt chúng hai góc đồng vị bằng nhau.
Như vậy qua điểm B ở ngoài đường thẳng a kẻ được 2 đường thẳng b và xy cùng song song với a. Theo tiên đề Ơclít thì đường thẳng xy trùng với đường thẳng b. Vậy \(\widehat {ABy}\) trùng với \(\widehat {{B_1}}\) nên \(\widehat {{A_1}} = \widehat {{B_1}}\)
Câu 44 trang 113 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Chứng minh rằng:
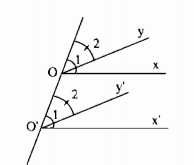
Nếu hai góc nhọn xOy và x’Oy’ có Ox // O’x’; Oy // O’y’ thì \(\widehat {xOy} = \widehat {x'Oy'}\).
Hướng dẫn: Sử dụng tính chất của hai đường thẳng song song.
Giải

Chứng minh:
Vẽ đường thẳng OO’
Vì Ox // O’x’ nên hai góc đồng vị \(\widehat {{O_1}}\) và \(\widehat {O{'_1}}\) bằng nhau.
Suy ra \(\widehat {{O_1}} = \widehat {O{'_1}}\) (1)
Vì Oy // O’y’ nên hai góc đồng vị \(\widehat {{O_2}}\) và \(\widehat {O{'_2}}\) bằng nhau.
Suy ra \(\widehat {{O_2}} = \widehat {O{'_2}}\) (2)
Từ (1) và (2) suy ra: \(\widehat {{O_1}} - \widehat {{O_2}} = \widehat {O{'_1}} - \widehat {O{'_2}}\)
Vậy \(\widehat {xOy} = \widehat {x'Oy'}\)
Giaibaitap.me
Giải bài tập trang 113, 114 bài ôn tập chương 1 đường thẳng vuông góc, đường thẳng song song Sách Bài Tập Toán lớp 7 tập 1. Câu 45: Vẽ hình theo trình tự sau...
Giải bài tập trang 137 bài 1 tổng ba góc của một tam giác Sách Bài Tập Toán lớp 7 tập 1. Câu 1: Tính giá trị x ở hình dưới...
Giải bài tập trang 137, 138 bài 1 tổng ba góc của một tam giác Sách Bài Tập Toán lớp 7 tập 1. Câu 5: Cho tam giác nhọn ABC. Kẻ BH vuông góc với AC (H ∈ AC) kẻ CK vuông góc với AB (K ∈ AB)...
Giải bài tập trang 138 bài 1 tổng ba góc của một tam giác Sách Bài Tập Toán lớp 7 tập 1. Câu 9: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC). Tìm góc bằng góc B....
