Câu 49 trang 46 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC cân tại A, D là trung điểm của BC. Gọi E và F là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh rằng DE = DF.

Giải

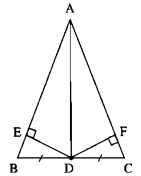
∆ABC cân tại A.

DB = DC (gt)

Nên đường trung tuyến AD cũng là đường phân giác của góc BAC.

\(\eqalign{
& DE \bot AB\left( {gt} \right) \cr
& DF \bot {\rm{A}}C\left( {gt} \right) \cr} \)

Suy ra: DE = DF (tính chất đường phân giác của góc).

Câu 50 trang 46 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC có Â = 70°, các đường phân giác BD, CE cắt nhau ở I. Tính \(\widehat {BIC}\).

Giải

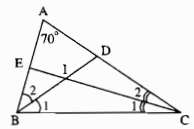
Trong ∆ABC ta có:

\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong tam giác)

\( \Rightarrow \widehat B + \widehat C = 180^\circ  - \widehat A = 180^\circ  - 70^\circ  = 110^\circ \

\(\widehat {{B_1}} = {1 \over 2}\widehat B\) (vì BD là tia phân giác)

\(\widehat {{C_1}} = {1 \over 2}\widehat C\) (vì CE là tia phân giác)

Trong ∆BIC ta có:

\(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng 3 góc trong tam giác)

\(\Rightarrow \widehat {BIC} = 180 - (\widehat {{B_1}} + \widehat {{C_1}})\)

\(\widehat {BIC} = 180^\circ  - {1 \over 2}(\widehat B + \widehat C) = 180^\circ  - {1 \over 2}.110^\circ  = 125^\circ \)

Câu 51 trang 46 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Tính góc A của tam giác ABC biết rằng các đường phân giác BD, CB cắt nhau tại I trong đó góc BIG bằng:

a) 120°

b) ∝(∝ > 90°)

Giải

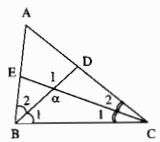
Trong ∆BIC ta có: \(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng 3 góc trong tam giác)

\(\Rightarrow \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ  - \widehat {BIC} = 180^\circ  - 120^\circ  = 60^\circ \)

      \(\widehat {{B_1}} = {1 \over 2}\widehat B\) (Vì BD là tia phân giác)

      \(\widehat {{C_1}} = {1 \over 2}\widehat C\) (Vì CE là tia phân giác)

              \( \Rightarrow \widehat B + \widehat C = 2\left( {\widehat {{B_1}} + \widehat {{C_1}}} \right) = 2.60^\circ  = 120^\circ \)

Trong ∆ABC ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong tam giác)

\( \Rightarrow \widehat A = 180^\circ  - (\widehat B + \widehat C) = 180^\circ  - 120^\circ  = 60^\circ \)

Câu 52 trang 46 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhau ở I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh rằng ba điểm B, I, K thẳng hàng.

Giải

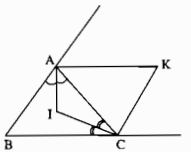
Kẻ \(IH \bot AB,IJ \bot BC,IG \bot AC\),

\(KD \bot AB,KE \bot AC,KF \bot BC\)

I nằm trên tia phân giác của \(\widehat {BAC}\)

\( \Rightarrow \) IH = IG (tính chất tia phân giác)

I nằm trên tia phân giác của \(\widehat {BCA}\)

\( \Rightarrow \) IG = IJ (tính chất tia phân giác)

Suy ra:  IH = IJ

Nên I nằm trên tia phân giác của \(\widehat {ABC}\)       (1)

     K nằm trên tia phân giác của \(\widehat {DAC}\)

\( \Rightarrow \) KD = KE (tính chất tia phân giác)

     K nằm trên tia phân giác của  \(\widehat {ACF}\)

\( \Rightarrow \) KE = KF (tính chất tia phân giác)

Suy ra: KD = KF => K nằm trên tia phân giác của \(\widehat {ABC}\)      (2)

Từ (1) và (2) suy ra: B, I, K thẳng hàng

Câu 53 trang 46 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC vuông tại A. Các tia phân  giác của các góc B và C cắt nhau tại I. Gọi D và E là chân các đường vuông góc kẻ từ I đến  AB và AC.

a) Chứng minh rằng AD = AE.

b) Tính các dộ dài AD, AE biết rằng AB = 6cm, AC = 8cm.

Giải

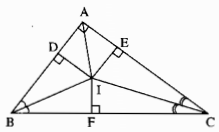
a) I là giao điểm phân giác trong của \(\widehat B\) và \(\widehat C\) nên AI là tia phân giác của Â.

\( \Rightarrow \) ID = IE (tính chất tia phân giác)         (1)

∆ADI vuông tại D có \(\widehat {DAI} = 45^\circ \)

Nên ∆ADI vuông cân tại D.

\( \Rightarrow \) ID = DA      (2)

∆AEI vuông tại E có \(\widehat {E{\rm{A}}I} = 45^\circ \)

Nên ∆ AEI vuông cân tại E

\( \Rightarrow \) IE = AE         (3)

Từ (1), (2) và (3) suy ra: AD = AE

b) Trong tam giác vuông ABC có Â=90°

Theo định lý Pitago ta có:

\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} \cr
& B{C^2} = {6^2} + {8^2} = 36 + 64 = 100 \cr} \)

\( \Rightarrow \) BC = 10 (cm)

Kẻ \(IF \bot BC\)

Xét hai tam giác vuông IDB và IFB:

\(\eqalign{
& \widehat {IDB} = \widehat {IFB} = 90^\circ \cr
& \widehat {DBI} = \widehat {FBI}\left( {gt} \right) \cr} \)

Cạnh huyền BI chung

Do đó:  ∆IDB = ∆IFB (cạnh huyền, góc nhọn)

\( \Rightarrow \) DB = FB           (4)

Xét hai tam giác vuông IEC và IFC:

\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)

Cạnh huyền CI chung  

Do đó: ∆IEC = ∆IFC (cạnh huyền, góc nhọn)

\( \Rightarrow \) CE = CF        (5)

AD + AE = AB – DB + AC – CE

\( \Rightarrow \) AD + AE = AB + AC – (DB + CF)          (6)

Từ (4), (5) và (6) suy ra:

AD + AE = AB + AC – (FB + FC) = AB + AC – BC

AD + AE = 6 + 8 – 10 = 4 (cm)

Mà AD = AE (chứng minh trên)

\( \Rightarrow \) AD = AE = 4: 2 = 2 (cm)

Giaibaitap.me