Câu 54 trang 47 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho ba tam giác cân ABC, DBC, EBC chung đáy BC. Chứng minh rằng ba điểm A, D, E thẳng hàng.
Giải
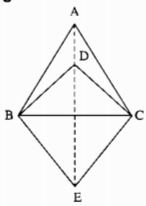
∆ABC cân tại A => AB = AC
Nên A thuộc đường trung trực của BC (1)
∆DBC cân tại D => DB = DC
Nên D thuộc đường trung trực của BC (2)
∆EBC cân tại E => EB = EC
Nên E thuộc đường trung trực của BC (3)
Từ (1), (2) và (3) suy ra: A, D, E thẳng hàng.
Câu 55 trang 47 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho hai điểm D, E nằm trên đường trung trực của đoạn thẳng BC. Chứng minh rằng ∆BDE = ∆CDE.
Giải
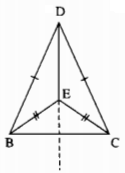
D thuộc đường trung trực của BC
\( \Rightarrow \) DB = DC (tính chất đường trung trực)
E thuộc đường trung trực của BC
\( \Rightarrow \) EB = EC (tính chất đường trung trực)
Xét ∆BDE = ∆CDE:
DB = DC (Chứng minh trên)
DE cạnh chung
EB = EC (chứng minh trên)
Do đó: ∆BDE = ∆CDE (c.c.c)
Câu 56 trang 47 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho đường thẳng d và hai điểm A, B thuộc cùng một nửa mặt phẳng có bờ d. Tìm một điểm C nằm trên d sao cho C cách đều A và B.
Giải
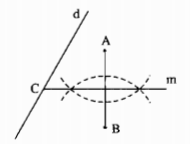
a) Nếu AB không vuông góc với d.
- Điểm C cách đều hai điểm A và B nên điểm C nằm trên đường trung trực của AB
- Điểm C ∈ d.
Vậy C là giao điểm của đường trung trực của AB và đường thẳng d.
Vậy dừng đường thẳng m là đường trung trực của đoạn thẳng AB cắt đường thẳng d tại C. Điểm C là điểm cần tìm.
b) Nếu \(AB \bot d\) thì đường trung trực của AB song song với đường thẳng d nên không tồn tại điểm C.
Câu 57 trang 47 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần I và II như hình sau. Cho điểm M thuộc phần I và điểm N thuộc phần II. Chứng minh rằng:
a) MA < MB
b) NA > NB
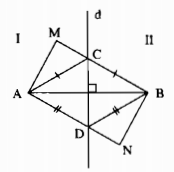
Giải
a) Nối MA, MB. Gọi C là giao điểm của MB với đường thẳng d, nối CA.
Ta có: MB = MC + CB
Mà CA = CB (tính chất đường trung trực)
Suy ra: MB = MC + CA (1)
Trong ∆ MAC ta có:
MA < MC + CA (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra: MA < MB
b) Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB.
Ta có: NA = ND + DB
Mà: DA = DB (tính chất đường trung trực)
Suy ra: NA = ND + DB (3)
Trong ∆NDB ta có:
NB < ND + DB (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA > NB
Giaibaitap.me
Giải bài tập trang 48, 49 bài 7 tính chất trung trực của một đoạn thẳng Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 7.1: Trên đường trung trực của đoạn thẳng AB, lấy hai điểm phân biệt M, N. Khi đó khẳng định nào sau đây đúng...
Giải bài tập trang 48 bài 7 tính chất trung trực của một đoạn thẳng Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 58: Cho hình 11. Chứng minh rằng AB vuông góc với CD...
Giải bài tập trang 48 bài 7 tính chất trung trực của một đoạn thẳng Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 61: Cho góc xOy bằng 60°, điểm A nằm trong góc xOy. Vẽ điểm B sao cho Ox là đường trung trực của AB. Vẽ điểm C sao cho Oy là đường trung trực của AC...
Giải bài tập trang 49 bài 7 tính chất trung trực của một đoạn thẳng Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 7.4: Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng...
