Bài 4.16 trang 69 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Cho hai tam giác ABC và DEF thoả mãn \(AB = DE,AC = DF,\widehat {BAC} = \widehat {EDF} = {60^\circ },BC = 6\;{\rm{cm}},\widehat {ABC} = {45^\circ }\). Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.

Lời giải: 

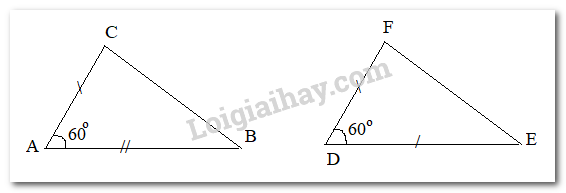
Xét hai tam giác ABC và DEF có:

\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} = {60^\circ }\end{array}\)

\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)

Do đó:

\(EF = BC = 6cm\)

\(\widehat {DEF} = \widehat {ABC} = {45^o}\)

\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)

\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)

Bài 4.17 trang 69 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Cho hai tam giác ABC và DEF thoả mãn \(AB = DE\), \(\widehat {ABC} = \widehat {DEF} = {70^\circ },\widehat {BAC} = \widehat {EDF} = {60^\circ },AC = 6\;{\rm{cm}}.\)

Tính độ dài cạnh DF.

Lời giải: 

Xét hai tam giác ABC và DEF có:

\(\begin{array}{l}\widehat {ABC} = \widehat {DEF} (= {70^\circ })\\AB = DE\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)

\( \Rightarrow \Delta ABC{\rm{  = }}\Delta DEF\)(g.c.g)

\( \Rightarrow DF = AC\)( 2 cạnh tương ứng)

Mà AC = 6 cm

\( \Rightarrow DF = 6cm\)

Bài 4.18 trang 69 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Cho Hình 4.44, biết \(EC = ED\) và \(\widehat {AEC} = \widehat {AED}\). Chứng minh rằng:

\(\begin{array}{*{20}{l}}{{\rm{ a) }}\Delta AEC = \Delta AED;}&{{\rm{ b) }}\Delta ABC = \Delta ABD.}\end{array}\)

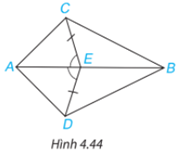
Lời giải: 

Bài 4.19 trang 69 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho \(\widehat {CAO} = \widehat {CBO}.\)

a) Chứng minh rằng \(\Delta OAC = \Delta OBC\).

b) Lấy điểm \(M\) trên tia đối của tia CO. Chứng minh rằng \(\Delta MAC = \Delta MBC\).

Lời giải: 

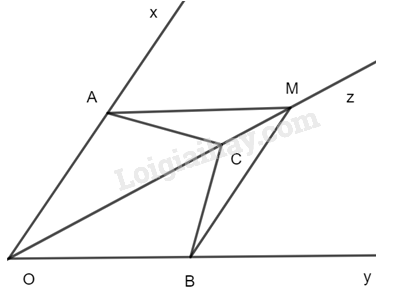
a)

Xét \(\Delta OAC\) và \(\Delta OBC\) có:

\(\widehat {AOC} = \widehat {AOB}\)(Oz là phân giác góc xOy)

OC chung

\(\widehat {CAO} = \widehat {CBO}.\)

\(\Rightarrow \Delta OAC = \Delta OBC\)(g.c.g)

b) Do \(\Delta OAC = \Delta OBC\) nên AC=BC ( 2 cạnh tương ứng)

Vì \(\widehat {ACO}\) và \(\widehat {ACM}\) kề bù

    \(\widehat {BCO}\) và \(\widehat {BCM}\) kề bù

Mà \(\widehat {ACO} = \widehat {BCO}\) nên \(\widehat {ACM} = \widehat {BCM}\)

Xét \(\Delta MAC\) và \(\Delta MBC\) có:

AC=BC

\(\widehat {ACM} = \widehat {BCM}\)

CM chung

\( \Rightarrow \Delta MAC = \Delta MBC\)(c.g.c)

Giaibaitap.me