Bài 4.33 trang 87 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Tính các số đo x, y trong tam giác dưới đây (H.4.75)

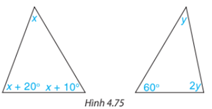
Lời giải: 

Áp dụng định lí tổng ba góc trong tam giác,

+) Ta có:

\(\begin{array}{l}x + x + {20^o} + x + {10^o} = {180^o}\\ \Rightarrow 3x = {150^o}\\ \Rightarrow x = {50^o}\end{array}\)

+) Ta có:

\(\begin{array}{l}y + {60^o} + 2y = {180^o}\\ \Rightarrow 3y = {120^o}\\ \Rightarrow y = {40^o}\end{array}\)

Bài 4.34 trang 87 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng\(\widehat {MAN} = \widehat {MBN}\).

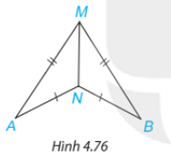
Lời giải: 

Xét 2 tam giác MNA và MNB có:

AM=BM

AN=BN

MN chung

=>\(\Delta MNA = \Delta MNB\) (c.c.c)

=>\(\widehat {MAN} = \widehat {MBN}\) (2 góc tương ứng)

Bài 4.35 trang 87 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Trong Hình 4.77, có AO = BO,\(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng AM = BN.

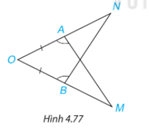
Lời giải: 

Xét 2 tam giác OAM và OBN có:

\(\widehat {OAM} = \widehat {OBN}\)

AO=BO

Góc O chung

=>\(\Delta OAM = \Delta OBN\)(g.c.g)

=>AM=BN (2 cạnh tương ứng)

Bài 4.36 trang 87 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Trong Hình 4.78, ta có AN = BM,\(\widehat {BAN} = \widehat {ABM}\). Chứng minh rằng\(\widehat {BAM} = \widehat {ABN}\).

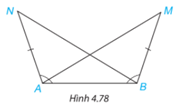
Lời giải: 

Xét 2 tam giác ANB và BMA có:

AN=BM

\(\widehat {BAN} = \widehat {ABM}\)

AB chung

=>\(\Delta ANB = \Delta BMA\)(c.g.c)

Bài 4.37 trang 87 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Theo em, tứ giác AMBN là hình gì?

Lời giải: 

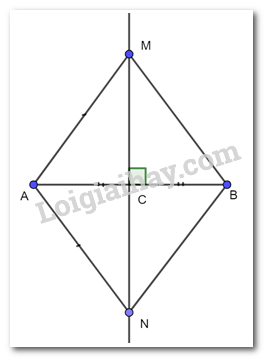
Vì M, N nằm trên đường trung trực của AB nên MA = MB ; NA = NB ( tính chất)

Mà MA = NA (gt)

Vậy MA = NA = MB = NB nên tứ giác AMBN là hình thoi

Bài 4.38 trang 87 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Cho tam giác ABC cân tại A có \(\widehat {A{\rm{ }}} = 120^\circ \). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:

a) \(\Delta \)BAM = \(\Delta \)CAN;

b) Các tam giác ANB, AMC lần lượt cân tại N, M.

Lời giải: 

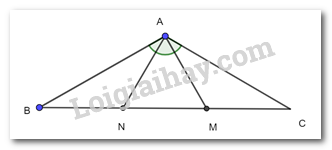
a) Xét 2 tam giác vuông BAM và CAN có:

AB=AC(Do tam giác ABC cân tại A)

\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)

=>\(\Delta BAM = \Delta CAN\)(g.c.g)

b)

Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:

\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).

Xét tam giác ABM vuông tại A có:

\(\begin{array}{l}\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\end{array}\)

Xét tam giác MAC có:

\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)

\(\Rightarrow \) Tam giác AMC cân tại M.

Vì \(\Delta BAM = \Delta CAN\)=>BM=CN => BN=MC

Xét 2 tam giác ANB và AMC có:

AB=AC

\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))

BN=MC

=>\(\Delta ANB = \Delta AMC\)(c.c.c)

Mà tam giác AMC cân tại M.

=> Tam giác ANB cân tại N.

Bài 4.39 trang 87 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng:

a) Tam giác CAM cân tại M;

b) Tam giác BAM là tam giác đều;

c) M là trung điểm của đoạn thẳng BC.

Lời giải: 

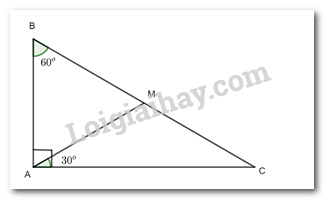
a)      Xét tam giác ABC có:

\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ =  > {90^o} + {60^o} + \widehat C = {180^o}\\ =  > \widehat C = {30^o}\end{array}\)

Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)

=>Tam giác CAM cân tại M.

b) Xét tam giác ABM có:

\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ =  > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ =  > \widehat {CMA} = {120^o}\\ =  > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)

Xét tam giác ABM có:

\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ =  > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ =  > \widehat {BAM} = {60^o}\end{array}\)

Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.

Giaibaitap.me