Bài 4.29 trang 86 sách giáo khoa Toán 7 Kết nối tri thức tập 1
Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ.
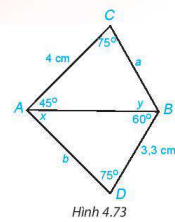
Lời giải:
Xét tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat C = {180^o}\\ \Rightarrow {45^o} + y + {75^o} = {180^o}\\ \Rightarrow y = {60^o}\end{array}\)
Xét tam giác ABD có:
\(\begin{array}{l}\widehat {DAB} + \widehat {DBA} + \widehat D = {180^o}\\ \Rightarrow x + {60^o} + {75^o} = {180^o}\\ \Rightarrow x = {45^o}\end{array}\)
Xét 2 tam giác ABC và ADB có:
\(\widehat {DAB} = \widehat {CAB} = {45^o}\)
AB chung
\(\widehat D = \widehat C = {75^o}\)
=>\(\Delta ABC = \Delta ADB\)(g.c.g)
=>BC=BD ( 2 cạnh tương ứng), mà BD = 3,3 cm =>a= BC= 3,3cm
AC=AD ( 2 cạnh tương ứng), mà AC = 4 cm =>b = AD = 4cm
Bài 4.30 trang 86 sách giáo khoa Toán 7 Kết nối tri thức tập 1
Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM =ON, OA > OM.
Chứng minh rằng:
a) \(\Delta \)OAN = \(\Delta \)OBM;
b) \(\Delta \)AMN = \(\Delta \)BNM.
Lời giải:
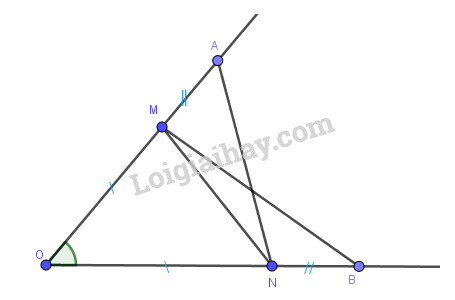
a) Xét tam giác OAN và OBM có:
OA=OB
\(\widehat{O}\) chung
OM=ON
=>\(\Delta OAN = \Delta OBM\)(c.g.c)
b) Do \(\Delta OAN = \Delta OBM\) nên AN=BM ( 2 cạnh tương ứng); \(\widehat {OAN} = \widehat {OBM}\)( 2 góc tương ứng) =>\(\widehat {NAM} = \widehat {MBN}\)
Do OA + AM = OM; OB + BN = ON
Mà OA = OB, OM =ON
=> AM=BN
Xét hai tam giác AMN và BNM có:
AN=BM
\(\widehat {NAM} = \widehat {MBN}\)
AM=BN
=>\(\Delta AMN = \Delta BNM\)(c.g.c)
Bài 4.31 trang 86 sách giáo khoa Toán 7 Kết nối tri thức tập 1
Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:
a) AC = BD;
b) \(\Delta \)ACD = \(\Delta \)BDC.
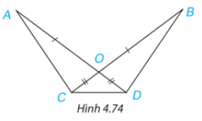
Lời giải:
Ta có: OA = OB, OC = OD nên AD=BC
Do OC=OD nên tam giác OCD cân => \(\widehat {OCD} = \widehat {ODC}\)
Xét 2 tam giác ACD và BDC có:
AD=BC
\(\widehat {OCD} = \widehat {ODC}\)
CD chung
=>\(\Delta ACD = \Delta BCD\)(c.g.c)
=>AC=BD (hai cạnh tương ứng)
b)Xét hai tam giác ACD và BDC có:
AO=BO
CO=DO
AC=BD
=>\(\Delta ACD = \Delta BDC\)(c.c.c)
Bài 4.32 trang 86 sách giáo khoa Toán 7 Kết nối tri thức tập 1
Cho tam giác MBC vuông tại M có \(\widehat B\) = 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
Lời giải:
Xét 2 tam giác vuông CMB và CMA có:
MC chung
MB=MA
=>\(\Delta CMB = \Delta CMA\)(c.g.c)
=>CA = CB (2 cạnh tương ứng).
=> Tam giác ABC cân tại C.
Mà góc B bằng 60o
=>Tam giác ABC đều.
Giaibaitap.me
Giải SGK Toán 7 trang 87 tập 1 Kết nối tri thức - Bài tập cuối chương 4: Tam giác bằng nhau. Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Theo em, tứ giác AMBN là hình gì?
Giải SGK Toán 7 trang 92 tập 1 Kết nối tri thức - Bài 17 Thu thập và phân loại dữ liệu. Bài 5.1 Với mỗi câu hỏi sau, hãy xác định xem dữ liệu thu được thuộc loại nào.
Giải SGK Toán 7 trang 99 tập 1 Kết nối tri thức - Bài 18: Biểu đồ hình quạt tròn. Bài 5.7 An khảo sát về thú nuôi được yêu thích của các bạn trong lớp và thu được kết quả như bảng sau
Giải SGK Toán 7 trang 105 tập 1 Kết nối tri thức - Bài 19: Biểu đồ đoạn thẳng. Bài 5.12 Bảng sau cho biết nhiệt độ tại thủ đô Hà Nội vào một ngày mùa thu.
