Câu 38 trang 25 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Tính f(x) + g(x) với:
\(f\left( x \right) = {x^5} - 3{{\rm{x}}^2} + {x^3} - {x^2} - 2{\rm{x}} + 5\)
\(g\left( x \right) = {x^2} - 3{\rm{x}} + 1 + {x^2} - {x^4} + {x^5}\)
Giải
Thu gọn rồi sắp xếp đa thức theo lũy thừa giảm của biến :
\(\eqalign{
& f\left( x \right) = {x^5} - 3{{\rm{x}}^2} + {x^3} - {x^2} - 2{\rm{x}} + 5 \cr
& \Leftrightarrow f(x) = {x^5} + {x^3} - {x^2} - 2{\rm{x}} + 5 \cr} \)
\(\eqalign{
& g\left( x \right) = {x^2} - 3{\rm{x}} + 1 + {x^2} - {x^4} + {x^5} \cr
& \Leftrightarrow g(x) = {x^5} - {x^4} + 2{x^2} - 3{\rm{x}} + 1 \cr} \)
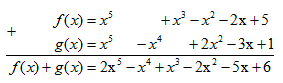
Câu 39 trang 25 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Tính f(x) – g(x) với :
\(f(x) = {x^7} - 3{{\rm{x}}^2} - {x^5} + {x^4} - {x^2} + 2{\rm{x}} - 7\)
\(g(x) = x - 2{{\rm{x}}^2} + {x^4} - {x^5} - {x^7} - 4{{\rm{x}}^2} - 1\)
Giải
Thu gọn rồi sắp xếp đa thức theo lũy thừa giảm của biến:
\(\eqalign{
& f(x) = {x^7} - 3{{\rm{x}}^2} - {x^5} + {x^4} - {x^2} + 2{\rm{x}} - 7 \cr
& \Leftrightarrow f(x) = {x^7} - {x^5} + {x^4} - 4{x^2} + 2{\rm{x}} - 7 \cr} \)
\(\eqalign{
& g(x) = x - 2{{\rm{x}}^2} + {x^4} - {x^5} - {x^7} - 4{{\rm{x}}^2} - 1 \cr
& \Leftrightarrow g(x) = - {x^7} - {x^5} + {x^4} - 6{{\rm{x}}^2} + x - 1 \cr} \)

Câu 40 trang 25 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho các đa thức:
\(f(x) = {x^4} - 3{{\rm{x}}^2} + x - 1\)
\(g(x) = {x^4} - {x^3} + {x^2} + 5\)
Tìm đa thức h(x) sao cho:
a) f(x) + h(x) = g(x)
b) f(x) - h(x) = g(x)
Giải
a) f (x) + h (x) = g (x)
\( \Rightarrow h(x) = g(x) - f(x) \)
\(h(x)= \left( {{x^4} - {x^3} + {x^2} + 5} \right) - ({x^4} - 3{{\rm{x}}^2} + x - 1)\)
\(\eqalign{
& h(x) = {x^4} - {x^3} + {x^2} + 5 - {x^4} + 3{{\rm{x}}^2} - x + 1 \cr
& h(x) = - {x^3} + 4{{\rm{x}}^2} - x + 6 \cr} \)
b) f (x) - h (x) = g (x)
\(\eqalign{
& \Rightarrow h(x) = f(x) - g(x) \cr
& \Leftrightarrow h(x) = ({x^4} - 3{{\rm{x}}^2} + x - 1) - ({x^4} - {x^3} + {x^2} + 5) \cr} \)
\(\eqalign{
& \Leftrightarrow h(x) = {x^4} - 3{{\rm{x}}^2} + x - 1 - {x^4} + {x^3} - {x^2} - 5 \cr
& \Leftrightarrow h(x) = {x^3} - 4{x^2} + x - 6 \cr} \)
Câu 41 trang 26 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho đa thức:
\(f(x) = {a_n}{x^n} + {a_{n - 1}}{x^{n - 1}} + ..... + {a_1}x + {a_0}\)
\(g(x) = {b_n}{x^n} + {b_{n - 1}}{x^{n - 1}} + ...... + {b_1}x + {b_0}\)
a) Tính f (x) + g (x)
b) Tính f (x) – g (x)
Giải
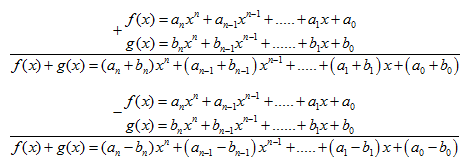
Giaibaitap.me
Giải bài tập trang 26 bài 8 cộng trừ đa thức một biến Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 42: Tính f (x) + g (x) – h (x) biết:...
Giải bài tập trang 26 bài 9 nghiệm của đa thức một biến Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 43: Chứng tỏ rằng...
Giải bài tập trang 26, 27 bài 9 nghiệm của đa thức một biến Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 46: Chứng tỏ rằng nếu a + b + c = 0 thì x = 1 là một nghiệm của đa thức...
Giải bài tập trang 27 bài 9 nghiệm của đa thức một biến Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 47: Chứng tỏ rằng nếu a – b + c = 0 thì x = -1 là một nghiệm của đa thức...
