Bài 3.1 trang 45 sách giáo khoa Toán 7 Kết nối tri thức tập 1

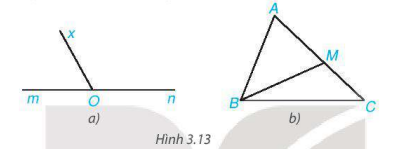
Cho Hình 3.13, hãy kể tên các cặp góc kề bù.

Lời giải: 

a) Góc xOm và xOn là 2 góc kề bù vì 2 góc này có chung cạnh Ox, cạnh Om là tia đối của On.

b) Góc AMB và CMB là 2 góc kề bù vì 2 góc này có chung cạnh MB, cạnh MA là tia đối của MC.

Bài 3.2 trang 45 sách giáo khoa Toán 7 Kết nối tri thức tập 1

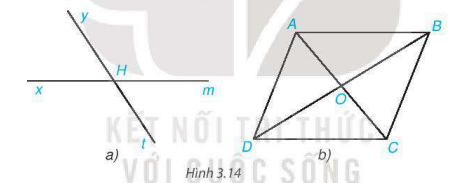
Cho Hình 3.14, hãy kể tên các cặp góc đối đỉnh.

Lời giải: 

a) 2 góc xHy và mHt là 2 góc đối đỉnh vì Hx và Hm là 2 tia đối nhau; Hy và Ht là 2 tia đối nhau.

2 góc xHt và mHy là 2 góc đối đỉnh vì Hx và Hm là 2 tia đối nhau; Ht và Hy là 2 tia đối nhau.

b) 2 góc AOB và COD là là 2 góc đối đỉnh vì OA và OC là 2 tia đối nhau; OB và OD là 2 tia đối nhau.

2 góc AOD và COB là là 2 góc đối đỉnh vì OA và OC là 2 tia đối nhau; OD và OB là 2 tia đối nhau.

Bài 3.3 trang 45 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Vẽ góc xOy có số đo bằng 60 \(^\circ \). Vẽ tia Om là tia đối của tia Ox.

a) Gọi tên hai góc kề bù có trong hình vừa vẽ.

b) Tính số đo góc yOm.

c) Vẽ tia Ot là tia phân giác của góc xOy. Tính số đo các góc tOy và tOm.

Lời giải: 

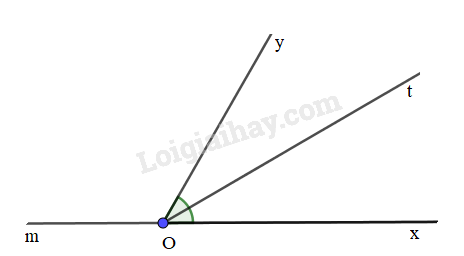
a) Hai góc kề bù có trên hình vừa vẽ là góc xOy và mOy

b) Vì \(\widehat {xOy} + \widehat {yOm} = 180^\circ \) (2 góc kề bù)

\(\begin{array}{l} \Rightarrow 60^\circ  + \widehat {yOm} = 180^\circ \\ \Rightarrow \widehat {yOm} = 180^\circ  - 60^\circ  = 120^\circ \end{array}\)

c) Vì tia Ot là tia phân giác của góc xOy nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ  = 30^\circ \)

Mà \(\widehat {xOt}\) và \(\widehat {tOm}\) là hai góc kề bù nên

\(\begin{array}{l}\widehat {xOt} + \widehat {tOm} = 180^\circ \\ \Rightarrow 30^\circ  + \widehat {tOm} = 180^\circ \\ \Rightarrow \widehat {tOm} = 180^\circ  - 30^\circ  = 150^\circ \end{array}\)

Vậy \(\widehat {tOy} = 30^\circ ;\widehat {tOm} = 150^\circ \)

Bài 3.4 trang 45 sách giáo khoa Toán 7 Kết nối tri thức tập 1

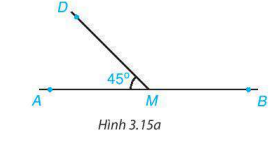
Cho Hình 3.15a, biết \(\widehat {DMA} = 45^\circ \). Tính số đo góc DMB

Lời giải: 

Vì góc AMD và BMD là hai góc kề bù nên

\(\begin{array}{l}\widehat {AMD} + \widehat {BMD} = 180^\circ \\ \Rightarrow 45^\circ  + \widehat {BMD} = 180^\circ \\ \Rightarrow \widehat {BMD} = 180^\circ  - 45^\circ  = 135^\circ \end{array}\)

Vậy \(\widehat {DMB} = 135^\circ \)

Bài 3.5 trang 45 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Cho Hình 3.15b, biết \(\widehat {xBm} = 36^\circ \). Tính số đo các góc còn lại trong hình vừa vẽ.

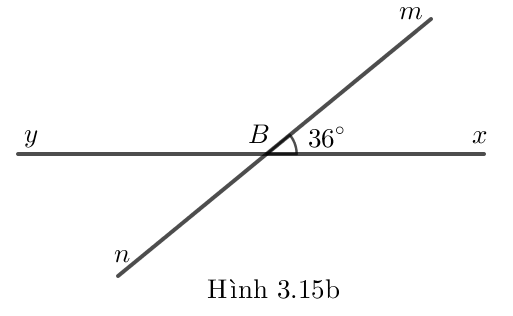
Lời giải: 

Vì \(\widehat{xBm}\) và \(\widehat{yBn}\) là hai góc đối đỉnh nên \(\widehat {xBm} = \widehat {yBn}\)

Mà \(\widehat {xBm} = 36^\circ \) nên \(\widehat {yBn} = 36^\circ \)

Vì \(\widehat{xBm}\) và \(\widehat{mBy}\) là hai góc kề bù nên

\(\begin{array}{l}\widehat {xBm} + \widehat {mBy} = 180^\circ \\ \Rightarrow 36^\circ  + \widehat {mBy} = 180^\circ \\ \Rightarrow \widehat {mBy} = 180^\circ  - 36^\circ  = 144^\circ \end{array}\)

Vì \(\widehat{mBy}\) và \(\widehat{nBx}\) là hai góc đối đỉnh nên \(\widehat {mBy} = \widehat {nBx}\)

Mà \(\widehat {mBy} = 144^\circ \) nên \(\widehat {nBx} = 144^\circ \)

Giaibaitap.me