Bài 2.27 trang 39 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Sử dụng máy tính cầm tay làm tròn các số sau đến chữ số thập phân thứ nhất:

\(a = \sqrt 2 ;b = \sqrt 5 \)

Tính tổng hai số thập phân nhận được.

Lời giải:

Ta có: a = 1,414…; b = 2,336

Làm tròn đến chữ số thập phân thứ nhất, ta được: \(a \approx 1,4;b \approx 2,2\)

Tổng 2 số thập phân nhận được là: 1,4 + 2,2 = 3,6

Bài 2.28 trang 39 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Dùng thước dây có vạch chia để đo độ dài đường gấp khúc ABC trong Hình 2.8 (đơn vị xentimet, làm tròn đến chữ số thập phân thứ nhất). So sánh kết quả với kết quả với kết quả của Bài tập 2.27.

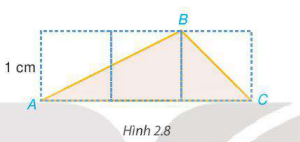
Lời giải:

Ta có: \(AB \approx 2,2(cm);BC  \approx 1,4(cm)\)

Vậy độ dài đường gấp khúc ABC là: \(AB + BC = 2,2 +1,4 = 3,6\) (cm)

Kết quả này trùng với kết quả ở bài tập 2.27

Bài 2.29 trang 39 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Chia sợi dây đồng dài 10 m thành 7 đoạn bằng nhau.

a) Tính độ dài mỗi đoạn dây nhận được, viết kết quả dưới dạng số thập phân vô hạn tuần hoàn.

b) Dùng 4 đoạn dây nhận được ghép thành một hình vuông. Gọi C là chu vi của hình vuông đó. Hãy tìm C bằng hai cách rồi so sánh kết quả:

Cách 1: Dùng thước dây có vạch chia để đo, lấy chính xác đến xentimet.

Cách 2: Tính \(C = 4.\frac{{10}}{7}\), viết kết quả dưới dạng số thập phân với độ chính xác 0,005.

Lời giải:

a) Mỗi đoạn dây nhận được là: \(\frac{{10}}{7} = 1,(428571)\) (m)

b) Cách 1: Dùng thước đo, ta được mỗi đoạn dây dài 143 cm.

Chu vi hình vuông là: 4.143 = 572 cm

Cách 2: \(C = 4.\frac{{10}}{7}\) \( = 5,(714285) \approx 5,71\)(m)

Chú ý:

Với 2 cách đo đạc và tính toán, ta có thể nhận được kết quả chênh lệch (không đáng kể), tùy vào cách làm tròn.

Bài 2.30 trang 39 sách giáo khoa Toán 7 Kết nối tri thức tập 1

a) Cho hai số thực a = -1,25 và b = -2,3. So sánh a và b, |a| và |b|.

b) Ta có nhận xét trong hai số âm, số nào có giá trị tuyệt đối lớn hơn là số bé hơn.

Em hãy áp dụng nhận xét này để so sánh -12,7 và -7,12.

Lời giải:

a) Vì 1,25 < 2,3 nên -1,25 > -2,3 hay a > b

\(\begin{array}{l}\left| a \right| = \left| { - 1,25} \right| = 1,25;\\\left| b \right| = \left| { - 2,3} \right| = 2,3\end{array}\)

Vì 1,25 < 2,3 nên \(\left| a \right| < \left| b \right|\).

b) Ta có -12,7  và -7,12 là các số âm, số -12,7 có giá trị tuyệt đối lớn hơn là số bé hơn nên -12,7 là số bé hơn.

Vậy  -12,7 < -7,12.

Bài 2.31 trang 39 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Cho hai số thực a = 2,1 và b = -5,2.

a) Em có nhận xét gì về hai tích a.b và -|a|.|b|?

b) Ta có cách nhân hai số khác dấu như sau: Muốn nhân hai số khác dấu ta nhân các giá trị tuyệt đối của chúng rồi đặt dấu “-“ trước kết quả.

Em hãy áp dụng quy tắc trên để tính (-2,5).3

Lời giải:

a) Ta có: a.b = 2,1. (-5,2) = -10,92

\(\begin{array}{l}\left| a \right| = 2,1;\left| b \right| = 5,2\\ \Rightarrow  - \left| a \right|.\left| b \right| =  - 2,1.5,2 =  - 10,92\end{array}\)

Nhận xét: a.b = -|a|.|b|

b) Ta có: -2,5 và 3 là số trái dấu và |-2,5| = 2,5; |3| = 3 nên (-2,5).3 = -(2,5.3) = -7,5

Giaibaitap.me