Câu 30 trang 141 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Tìm chỗ sai trong bài làm sau đây của một học sinh (hình dưới).
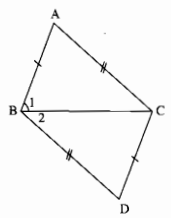
∆ABC = ∆DCB (c.c.c)
\( \Rightarrow \widehat {{B_1}} = \widehat {{B_2}}\) (cặp góc tương ứng)
\( \Rightarrow \) BC là tia phân giác của góc ABD
Giải
Bạn học sinh suy luận ∆ABC = ∆DCB
\( \Rightarrow \widehat {{B_1}} = \widehat {{B_2}}\) là sai vì \(\widehat {{B_1}}\) và \(\widehat {{B_2}}\) không phải là hai góc tương ứng của hai tam giác bằng nhau nói trên. Do đó không suy ra được BC là tia phân giác của góc ABD.
Câu 31 trang 141 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Vẽ tam giác ABC có AB = AC = 6cm, BC = 2cm. Sau đó đo góc A để kiểm tra rằng \(\widehat A \approx 20^\circ \).
Giải
Hình vẽ:
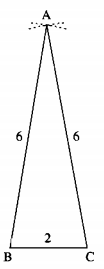
Ta có \(\widehat A \approx 20^\circ \)
Câu 32 trang 141 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Tam giác ABC có AB = AC, M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC.
Giải
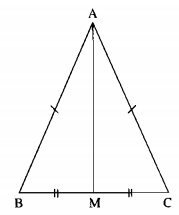
Xét ∆AMB và ∆AMC, ta có ;
AB = AC (gt)
BM = CM (vì M là trung điểm BC)
AM cạnh chung
Suy ra: ∆AMB = ∆AMC (c.c.c)
\( \Rightarrow \widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng)
Ta có: \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (hai góc kề bù)
Suy ra: \(\widehat {AMB} = \widehat {AMC} = 90^\circ \).Vậy \(AM \bot BC\)
Giaibaitap.me
Giải bài tập trang 141 bài 3 trường hợp bằng nhau thứ nhất của tam giác cạnh-cạnh-cạnh (c-c-c) Sách Bài Tập Toán lớp 7 tập 1. Câu 33: Cho đoạn thẳng AB. Vẽ cung tròn tâm A bán kính AB và cung tròn tâm B bán kính BA, chúng cắt nhau ở C và D...
Giải bài tập trang 142 bài 4 trường hợp bằng nhau thứ nhất của tam giác cạnh-góc-cạnh (c-g-c) Sách Bài Tập Toán lớp 7 tập 1. Câu 36: Vẽ tam giác ABC biết BA = BC = 2,5cm...
Giải bài tập trang 142 bài 4 trường hợp bằng nhau thứ nhất của tam giác cạnh-góc-cạnh (c-g-c) Sách Bài Tập Toán lớp 7 tập 1. Câu 40: Qua trung điểm M của đoạn thẳng AB, kẻ đường thẳng vuông góc với AB...
Giải bài tập trang 142, 143 bài 4 trường hợp bằng nhau thứ nhất của tam giác cạnh-góc-cạnh (c-g-c) Sách Bài Tập Toán lớp 7 tập 1. Câu 43: So sánh các độ dài DA và DE...
