Bài 1.26 trang 22 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Tìm x, biết:

\(\begin{array}{l}a)x + 0,25 = \frac{1}{2}\\b)x - \left( { - \frac{5}{7}} \right) = \frac{9}{{14}}\end{array}\)

Lời giải:

\(\begin{array}{l}a)x + 0,25 = \frac{1}{2}\\x = \frac{1}{2} - 0,25\\x = \frac{1}{2} - \frac{1}{4}\\x = \frac{2}{4} - \frac{1}{4}\\x = \frac{1}{4}\end{array}\)

Vậy \(x = \frac{1}{4}\)

\(\begin{array}{l}b)x - \left( { - \frac{5}{7}} \right) = \frac{9}{{14}}\\x = \frac{9}{{14}} + \left( { - \frac{5}{7}} \right)\\x = \frac{9}{{14}} + \left( { - \frac{{10}}{{14}}} \right)\\x = \frac{{ - 1}}{{14}}\end{array}\)

Vậy \(x = \frac{{ - 1}}{{14}}\)

Bài 1.27 trang 22 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Tìm x, biết:

\(\begin{array}{l}a)x - \left( {\frac{5}{4} - \frac{7}{5}} \right) = \frac{9}{{20}}\\b)9 - x = \frac{8}{7} - \left( { - \frac{7}{8}} \right)\end{array}\)

Lời giải:

\(\begin{array}{l}a)x - \left( {\dfrac{5}{4} - \dfrac{7}{5}} \right) = \dfrac{9}{{20}}\\x = \dfrac{9}{{20}} + \left( {\dfrac{5}{4} - \dfrac{7}{5}} \right)\\x = \dfrac{9}{{20}} + \dfrac{{25}}{{20}} - \dfrac{{28}}{{20}}\\x = \dfrac{{6}}{{20}}\\x = \dfrac{{ 3}}{{10}}\end{array}\)

Vậy \(x = \dfrac{{ 3}}{{10}}\)

\(\begin{array}{*{20}{l}}{b)9 - x = \dfrac{8}{7} - \left( { - \dfrac{7}{8}} \right)}\\\begin{array}{l}9 - x = \dfrac{8}{7} + \dfrac{7}{8}\\9 - x = \dfrac{{64}}{{56}} + \dfrac{{49}}{{56}}\\9 - x = \dfrac{{113}}{{56}}\end{array}\\{x = 9 - \dfrac{{113}}{{56}}}\\{x = \dfrac{{504}}{{56}} - \dfrac{{113}}{{56}}}\\{x = \dfrac{{391}}{{56}}}\end{array}\)

Vậy \(x = \dfrac{{391}}{{56}}\)

Bài 1.28 trang 22 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Tính một cách hợp lí.

\(\begin{array}{l}a) - 1,2 + ( - 0,8) + 0,25 + 5,75 - 2021\\b) - 0,1 + \frac{{16}}{9} + 11,1 + \frac{{ - 20}}{9}\end{array}\)

Lời giải:

\(\begin{array}{l}a) - 1,2 + ( - 0,8) + 0,25 + 5,75 - 2021\\ = [ - 1,2 + ( - 0,8)] + (0,25 + 5,75) - 2021\\ = ( - 2) + 6 - 2021\\ = 4 - 2021\\ =  - 2017\\b) - 0,1 + \frac{{16}}{9} + 11,1 + \frac{{ - 20}}{9}\\ = [( - 0,1) + 11,1] + \left( {\frac{{16}}{9} + \frac{{ - 20}}{9}} \right)\\ = 11 + \frac{{ - 4}}{9}\\ = \frac{{99}}{9} + \frac{{ - 4}}{9}\\ = \frac{{95}}{9}\end{array}\)

Bài 1.29 trang 22 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Bỏ dấu ngoặc rồi tính các tổng sau:

\(\begin{array}{l}a)\frac{{17}}{{11}} - \left( {\frac{6}{5} - \frac{{16}}{{11}}} \right) + \frac{{26}}{5}\\b)\frac{{39}}{5} + \left( {\frac{9}{4} - \frac{9}{5}} \right) - \left( {\frac{5}{4} + \frac{6}{7}} \right)\end{array}\)

Lời giải:

\(\begin{array}{l}a)\frac{{17}}{{11}} - \left( {\frac{6}{5} - \frac{{16}}{{11}}} \right) + \frac{{26}}{5}\\ = \frac{{17}}{{11}} - \frac{6}{5} + \frac{{16}}{{11}} + \frac{{26}}{5}\\ = (\frac{{17}}{{11}} + \frac{{16}}{{11}}) + (\frac{{26}}{5} - \frac{6}{5})\\ = \frac{{33}}{{11}} + \frac{{20}}{5}\\ = 3 + 4\\ = 7\\b)\frac{{39}}{5} + \left( {\frac{9}{4} - \frac{9}{5}} \right) - \left( {\frac{5}{4} + \frac{6}{7}} \right)\\ = \frac{{39}}{5} + \frac{9}{4} - \frac{9}{5} - \frac{5}{4} - \frac{6}{7}\\ = (\frac{{39}}{5} - \frac{9}{5}) + (\frac{9}{4} - \frac{5}{4}) - \frac{6}{7}\\ = \frac{{30}}{5} + \frac{4}{4} - \frac{6}{7}\\ = 6 + 1 - \frac{6}{7}\\ = 7 - \frac{6}{7}\\ = \frac{{49}}{7} - \frac{6}{7}\\ = \frac{{43}}{7}\end{array}\)

Bài 1.30 trang 22 sách giáo khoa Toán 7 Kết nối tri thức tập 1

Để làm một cái bánh, cần \(2\frac{3}{4}\) cốc bột. Lan đã có \(1\frac{1}{2}\) cốc bột. Hỏi Lan cần thêm bao nhiêu cốc bột nữa?

Lời giải:

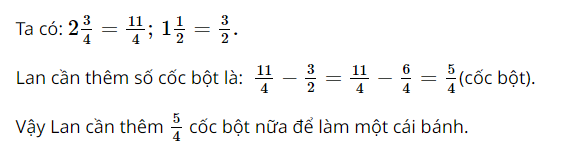
 Giaibaitap.me