Bài 1 trang 35 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho hai đa thức P(x) = \( - 3{x^4} - 8{x^2} + 2x\) và Q(x) = \(5{x^3} - 3{x^2} + 4x - 6\).

Hãy tính P(x) + Q(x) và P(x) – Q(x).

Lời giải:

\(P(x) + Q(x) =  - 3{x^4} - 8{x^2} + 2x + 5{x^3} - 3{x^2} + 4x - 6\)

\( =  - 3{x^4} + 5{x^3} + ( - 8{x^2} - 3{x^2}) + (2x + 4x) - 6\)

\( =  - 3{x^4} + 5{x^3} - 11{x^2} + 6x - 6\)

\(P(x) - Q(x) =  - 3{x^4} - 8{x^2} + 2x - 5{x^3} + 3{x^2} - 4x + 6\)

\( =  - 3{x^4} - 5{x^3} + ( - 8{x^2} + 3{x^2}) + (2x - 4x) + 6\)

\( =  - 3{x^4} - 5{x^3} - 5{x^2} - 2x + 6\)

Bài 2 trang 35 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho đa thức M(x) = \(7{x^3} - 2{x^2} + 8x + 4\)

Tìm đa thức N(x) sao cho M(x) + N(x) =  \(3{x^2} - 2x\)

Lời giải:

Vì M(x) + N(x) = \(3{x^2} - 2x\)

Mà M(x) = \(7{x^3} - 2{x^2} + 8x + 4\)

Ta có: N(x) = M(x) + N(x) – M(x)

= \(3{x^2} - 2x - 7{x^3} + 2{x^2} - 8x - 4\)

\( =  - 7{x^3} + 5{x^2} - 10x - 4\)

Bài 3 trang 36 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho đa thức A(y) = \( - 5{y^4} - 4{y^2} + 2y + 7\)

Tìm đa thức B(y) sao cho B(y) – A(y) = \(2{y^3} - 9{y^2} + 4y\)

Lời giải:

\(B(y) - A(y) = 2{y^3} - 9{y^2} + 4y\)

\(\begin{array}{l}A(y) =  - 5{y^4} - 4{y^2} + 2y + 7\\ \Rightarrow B(y) = 2{y^3} - 9{y^2} + 4y - 5{y^4} - 4{y^2} + 2y + 7\\ =  - 5{y^4} + 2{y^3} - 13{y^2} + 6y + 7\end{array}\)

Bài 4 trang 36 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Viết biểu thức biểu thị chu vi của hình thang cân trong Hình 3.

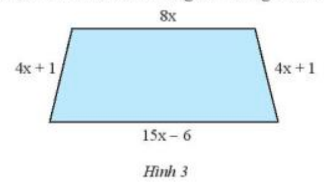
Lời giải:

Ta có chu vi hình thang là :

C = \(8x + (15x - 6) + (4x + 1) + (4x + 1)\)

\( = 31x - 4\)

Bài 5 trang 36 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho tam giác (xem Hình 4) có chu vi bằng 12t – 3. Tìm cạnh chưa biết của tam giác đó.

Lời giải:

Ta có chu vi hình tam giác là :12t – 3

Cạnh cần tìm là : 12t – 3 – (3t + 8) – (4t – 7) = 5t – 4

Bài 6 trang 36 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho ba đa thức P(x) = \(9{x^4} - 3{x^3} + 5x - 1\)

Q(x) = \( - 2{x^3} - 5{x^2} + 3x - 8\)và R(x) = \( - 2{x^4} + 4{x^2} + 2x - 10\)

Tính P(x) + Q(x) + R(x) và P(x) – Q(x) – R(x)

Lời giải:

P(x)+Q(x)+R(x) = \(9{x^4} - 3{x^3} + 5x - 1 - 2{x^3} - 5{x^2} + 3x - 8 - 2{x^4} + 4{x^2} + 2x - 10\)

\(\begin{array}{l} = (9{x^4} - 2{x^4})+( - 3{x^3} - 2{x^3})+( - 5{x^2} + 4{x^2}) +( 5x + 3x + 2x)+( - 8 - 10 - 1)\\ = 7{x^4} - 5{x^3} - {x^2} + 10x - 19\end{array}\)

P(x)-Q(x)-R(x) = \(9{x^4} - 3{x^3} + 5x - 1 + 2{x^3} + 5{x^2} - 3x + 8 + 2{x^4} - 4{x^2} - 2x + 10\)

\(\begin{array}{l} = (9{x^4} + 2{x^4})+( - 3{x^3} + 2{x^3} )+ (5{x^2} - 4{x^2}) + (5x - 3x - 2x) + (10 - 1 + 8)\\ = 11{x^4} - {x^3} + {x^2} + 17\end{array}\)

Bài 7 trang 36 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho đa thức \(P(x) = {x^3} - 4{x^2} + 8x - 2\). Hãy viết P(x) thành tổng của hai đa thức bậc bốn

Lời giải: 

\(\begin{array}{l}P(x) = {x^3} - 4{x^2} + 8x - 2\\ = {x^3} - 4{x^2} + 8x - 2 + {x^4} - {x^4}\\ = {x^4} + {x^3} - 4{x^2} + 8x - 2 - {x^4}\\ = ({x^4} + {x^3} - 4{x^2} + 8x - 2) + ( - {x^4})\end{array}\)

Bài 8 trang 36 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho hình vuông cạnh 2x và bên trong là hình chữ nhật có độ dài hai cạnh là x và 3 (Hình 5). Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh

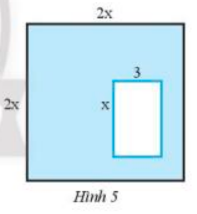
Lời giải: 

Diện tích hình vuông là : \(2x.2x = 4{x^2}\)

Diện tích hình chữ nhật là : \(3.x = 3x\)

Diện tích phần cần tìm là : \(4{x^2} - 3x\)

Bài 9 trang 36 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

a) Thực hiện phép tính: \((3x - 1) + \left[ {(2{x^2} + 5x) + (4 - 3x)} \right]\)

b) Cho A = 4x + 2, C = \(5 - 3{x^2}\). Tìm đa thức B sao cho A + B = C

Lời giải:

a)   (3x - 1) + [(2x² + 5x) + (4 - 3x)]

= 3x - 1 + 2x² + 5x + 4 - 3x

= 2x² + (3x + 5x - 3x) + (-1 + 4)

= 2x² + 5x + 3

b) Do A + B = C nên B = C - A

B = 5 - 3x² - (4x + 2)

B = 5 - 3x² - 4x - 2

B = -3x² - 4x + (5 - 2)

B = -3x² - 4x + 3

Vậy B = -3x² - 4x + 3.

Giaibaitap.me