Câu 7 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. So sánh \(\widehat {BAM}\) và \(\widehat {CAM}\).

Giải

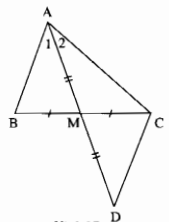
Trên tia đối tia MA lấy điểm D sao cho MD = MA.

Xét ∆AMB và ∆DMC:

                 MA = MD (theo cách vẽ)

                 \(\widehat {AMB} = \widehat {DMC}\) (đối đỉnh)

                 MB = MC (gt)

Do đó: ∆AMB = ∆DMC (c.g.c)

Nên: AM = CD (2 cạnh tương ứng)

         \(\widehat D = \widehat {{A_1}}\) (2 góc tương ứng)           (1)

          AB < AC (gt)

Suy ra: CD < AC

Trong ∆ADC ta có: CD < AC

Nên \(\widehat D = \widehat {{A_2}}\) (đối diện cạnh lớn hơn là góc lớn hơn)       (2)

Từ (1) và  (2) suy ra: \(\widehat {{A_1}} = \widehat {{A_2}}\) hay \(\widehat {BAM} > \widehat {MAC}\)

Câu 8 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC ở D. So sánh các độ dài BD, DC.

Giải

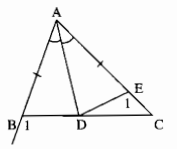
Trên cạnh AC lấy điểm E sao cho AE = AB

AB < AC nên AE < AC => E nằm giữa A và C

Xét ∆ABD và ∆AED:

                        AB = AE (theo cách vẽ)      

                       \(\widehat {BA{\rm{D}}} = \widehat {E{\rm{AD}}}\left( {gt} \right)\)

                        AD cạnh chung

Do đó: ∆ABD = ∆AED (c.g.c)

=> BD = DE (2 cạnh tương ứng)

\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {A{\rm{ED}}}\) (2 góc tương ứng)

\(\widehat {AB{\rm{D}}} + \widehat {{B_1}} = 180^\circ \) (2 góc kề bù)

\(\widehat {A{\rm{ED}}} + \widehat {{E_1}} = 180^\circ \) (2 góc kề bù)

Suy ra: \(\widehat {{B_1}} = \widehat {{E_1}}\)

Trong ∆ABC ta có \(\widehat {{B_1}}\) là góc ngoài tại đỉnh B.

\( \Rightarrow \widehat {{B_1}} > \widehat C\) (tính chất góc ngoài tam giác)

Suy ra: \(\widehat {{E_1}} > \widehat C\)

Trong ∆DEC ta có: \(\widehat {{E_1}} > \widehat C\)

\( \Rightarrow \) DC > DE  (đối diện góc lớn hơn là cạnh lớn hơn)

Suy ra: BD < DC.

Câu 9 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Chứng minh rằng nếu một tam giác vuông có một góc nhọn bằng 30°  thì cạnh góc vuông đối diện với nó bằng nửa cạnh huyền.

Giải

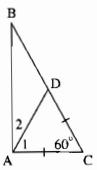
Xét ∆ABC có \(\widehat A = 90^\circ ;\widehat B = 30^\circ \)

Trên cạnh BC lấy điểm D sao cho CD = AC

Suy ra: ∆ACD cân tại C

Mà \(\widehat C + \widehat B = 90^\circ \) (tính chất tam giác vuông)

\( \Rightarrow \widehat C = 90^\circ  - \widehat B = 90^\circ  - 30^\circ  = 60^\circ \)

Suy ra: ∆ACD đều

\( \Rightarrow \) AC = AD = DC và \(\widehat {{A_1}} = 60^\circ \)

\(\widehat {{A_1}} + \widehat {{A_2}} = \widehat {BAC} = 90^\circ  \Rightarrow \widehat {{A_2}} = 90^\circ  - \widehat {{A_1}} = 90^\circ  - 60^\circ  = 30^\circ \)

Trong ∆ADB ta có: \(\widehat {{A_2}} = \widehat B = 30^\circ \)

Suy ra: ∆ADB cân tại D (vì có 2 góc kề cạnh AB bằng nhau)

\( \Rightarrow \) AD = DB

Suy ra: AC = CD = DB mà CD + DB = BC

Vậy \(AC = {1 \over 2}BC\)

Câu 10 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Chứng minh rằng định lý “Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn” theo gợi ý sau:

Cho tam giác ABC có \(\widehat B > \widehat C\)

a) Có thể xảy ra AC < AB hay không ?

b) Có thể xảy ra AC = AB hay không ?

Giải

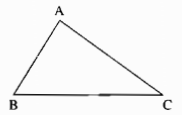
a) Nếu AB > AC thì \(\widehat C > \widehat B\) (góc đối diện với cạnhlớn hơn là góc lớn hơn)

Điều này trái với giả thiết \(\widehat B > \widehat C\)

b) Nếu AB = AC thì ∆ABC cân tại A.

\(\Rightarrow \widehat B = \widehat C\) (tính chất tam giác cân)

Điều này trái với giả thiết \(\widehat B > \widehat C\)

Vậy: \(\widehat B > \widehat C\) thì AC > AB

Giaibaitap.me