Câu 7.4 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng:
a) D là trung điểm của cạnh BC.
b) \(\widehat A = \widehat B + \widehat C\)
Giải
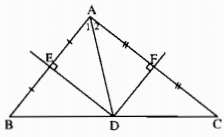
a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b) Ta có ∆DEB = ∆DEA(c.g.c) nên \(\widehat B = \widehat {{A_1}}\). Tương tự \(\widehat C = \widehat {{A_2}}\).
Suy ra \(\widehat A = \widehat {{A_1}} + \widehat {{A_2}} = \widehat B + \widehat C\)
Câu 7.5 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Chứng minh rằng nếu trong tam giác ABC có hai cạnh AB và AC không bằng nhau thì đường trung tuyến xuất phát từ đỉnh A không vuông góc với BC.
Giải
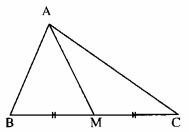
Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC.
Giả sử \(AM \bot BC\). Khi đó AM là đường trung trực của đoạn thẳng BC. Suy ra A = AC. Điều này mâu thuẫn với giả thiết AB # AC. Vậy trung tuyến AM không vuông góc với BC.
Câu 7.6 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho đường thẳng d và hai điểm A, B nằm về một phía của d sao cho AB không vuông góc với d. Hãy tìm trên d một điểm M sao cho \(\left| {MA - MB} \right|\) có giá trị nhỏ nhất.
Giải
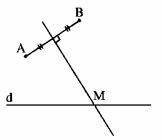
Ta có \(\left| {MA - MB} \right| \ge 0\) với một điểm M tùy ý và \(\left| {MA - MB} \right| = 0\) chỉ với các điểm M mà MA = MB, tức là chỉ với các điểm M nằm trên đường trung trực của đoạn thẳng AB.
Mặt khác M phải thuộc d. Vậy M là giao điểm của đường thẳng d và đường trung trực của đoạn thẳng AB. Có giao điểm này vì AB không vuông góc với d.
Tóm lại: Khi M là giao điểm của d và đường trung trực của đoạn thẳng AB thì \(\left| {MA - MB} \right|\) đạt giá trị nhỏ nhất và bằng 0.
Giaibaitap.me
Giải bài tập trang 49 bài 8 tính chất ba đường trung trực của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 64: Cho tam giác ABC. Tìm một điểm O cách đều ba điểm A, B, C...
Giải bài tập trang 50 bài 8 tính chất ba đường trung trực của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 8.1: Cho tam giác cân (không đều) ABC có AB = AC. Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. ...
Giải bài tập trang 50 bài 8 tính chất ba đường trung trực của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 67: Có một chi tiết máy (mà đường viền ngoài là đường tròn) bị gẫy (hình bên). Hãy nêu cách xác định tâm của đường viền...
Giải bài tập trang 50, 51 bài 9 tính chất ba đường cao của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 70: Cho tam giác ABC vuông tại B. Điểm nào là trực tâm của tam giác đó?...
