Bài 40 trang 73 sgk toán lớp 7- tập 2

Cho tam giác ABC cân tại A. gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng

Hướng dẫn:

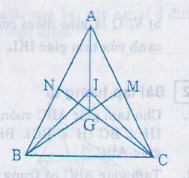
Gọi giao điểm của BG với AC là M;

CG với AB là N

Vì G là trọng tâm của ∆ ABC

nên BM, CN, là trung tuyến

Mặt khác ∆ABC cân tại A

Nên BM = CN 

Ta có GB = \(\frac{1}{2}\)BM; GC = \(\frac{2}{3}\)CN (t/c trọng tâm của tam giác)

Mà BM = CN nên GB = GC

Do đó: ∆AGB = ∆AGC (c.c.c)

=> \(\widehat{BAG}= \widehat{CAG}\)  => G thuộc phân giác của \(\widehat{BAC}\)

Mà ∆ABI = ∆ACI (c.c.c)

=> \(\widehat{BAI}= \widehat{CAI}\) => I thuộc phân giác của \(\widehat{BAC}\)

Vì G, I cùng thuộc phân giác của \(\widehat{BAC}\) nên A, G, I  thẳng hàng

Bài 41 trang 73 sgk toán lớp 7- tập 2

 Hỏi trọng tâm của một tam giác đều có cách đều ba cạnh của nó hay không ? Vì sao ?

Hướng dẫn:

Trọng tâm của tam giác đều cách đều ba cạnh của nó :

Giả sử ∆ABC đều có trọng tâm G

=> GA = \(\frac{2}{3}\)AN; GB = \(\frac{2}{3}\)BM; GC = \(\frac{2}{3}\)EC

Vì ∆ABC đều nên ba trung tuyến AN, BM, CE bằng nhau

=> GA = GB = GC

Do đó: ∆AMG = ∆CMG (c.c.c)

=> \(\widehat{AMG}=\widehat{CMG}\)

Mà \(\widehat{AMG}=\widehat{CMG}\) = 180⁰

=> \(\widehat{AMG}\) =  90⁰

=> GM ⊥ AC tức là GM khoảng cách từ G đến AC

Chứng minh tương tự GE, GN là khoảng cách từ G đến AB, AC

Mà GM =\(\frac{1}{3}\)BM; GN = \(\frac{1}{3}\)AN; EG = \(\frac{1}{3}\)EC

Và AN = BM = EC nên GM = GN = GE

Hay G cách đều ba cạnh của tam giác ABC

Bài 42 trang 73 sgk toán lớp 7- tập 2

Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân

Gợi ý : Trong ∆ABC, nếu AD vừa là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn AD₁ sao cho DA₁ = AD

Hướng dẫn:

Giả sử  ∆ABC có AD là phân giác \(\widehat{BAC}\) và DB = DC, ta chứng minh  ∆ABC  cân tại A

Kéo dài AD một đoạn DA₁ = AD

Ta có:   ∆ADC =  ∆A₁DC (c.g.c)

Nên \(\widehat{BAD}= \widehat{CA_{1}D}\)

mà \(\widehat{BAD}= \widehat{CAD}\) (gt)

=> \(\widehat{CAD}= \widehat{CA_{1}D}\)

=>   ∆ACA₁ cân tại C

Ta lại có: AB = A₁C ( ∆ADB = ∆A₁DC)

              AC = A₁C ( ∆ACA₁ cân tại C)

=> AB = AC

Vậy  ∆ABC cân tại A

Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân

Bài 43 trang 73 sgk toán lớp 7- tập 2

Đố : Có hai con đường cắt nhau và cùng cắt một con sông tại hai điểm khác nhau.

Hãy tìm một địa điểm để xây dựng một đài quan sát sao cho khoảng cách từ đó đến hai con đường và đến bờ sông bằng nhâu. Có tất cả mấy địa điểm như vậy ? 

Hướng dẫn:

Hai con đường cắt nhau và cùng cắt một con song tạo thành tam giác ABC. Địa điểm để xây dựng trạm kiểm lâm thỏa mãn đề bài phải là giao điểm I của ba đường phân giác trong của tam giác ABC và giao điểm K của tia phân giác của góc A và hai tia phân giác của các góc ngoài ở đỉnh D và đỉnh E của tam giác ADE.

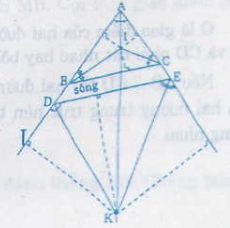
Vậy các địa điểm và các khoảng cách này ngắn nhất để xây dựng trạm kiểm lâm là I, K

Giaibaitap.me