Bài 1 trang 90 sgk toán 7 tập 2

Cho điểm M và hai đường thẳng a, b không song song với nhau (h.59)

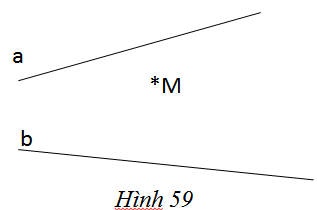
a) Vẽ đường thẳng MH vuông góc với a (H ∈ a) , MK vuông góc với b (K ∈ b). Nêu cách vẽ.

b) Qua M vẽ đường thẳng xx’ song song với a và đường thẳng yy’ song song với b. Nêu cách vẽ.

c) Viết tên các cặp góc bằng nhau, bù nhau.

Hướng dẫn làm bài:

a) Trước hết, ta nêu cách vẽ một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

1.Cách vẽ dùng ê ke và thước kẻ:

+Cho trước đường thẳng p và M ∉ p.

Đặt một lề ê ke trùng với p, dịch chuyển ê ke trên p sao cho lề thứ hai của ê ke sát vào M 

+Cho trước đường thẳng p và  \(M \in p\)

 Đặt một lề ê ke trùng với p và dịch chuyển ê ke trên p sao cho góc ê ke trùng với M.

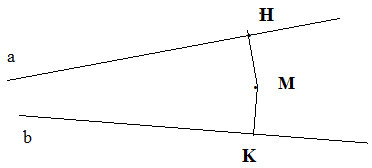
2.Cách vẽ dùng compa và thước kẻ:

+Cho trước đường thẳng p và M ∉ p.

Vẽ đường thẳng qua M vuông góc với p.

Chọn trên p hai điểm A và B.

Vẽ các đường tròn (A; AM) và (B; BM)

Hai đường tròn này cắt nhau tại M và M’ thì NM’ vuông góc với p 

Chú ý: Có thể xem bài tập 51 phần hình học. Cho trước đường thẳng p và

Vẽ đường thẳng vuông góc với p tại M 

Dùng compa vẽ đường tròn (M; r₁) cắt p tại A và B. Vẽ các đường tròn (A;r₂) và (B; r₂) với r₂ > r₁.

Các đường tròn này cắt nhau tại E và F thì đường thẳng EF vuông góc p tại M. Bây giờ ta theo một trong hai cách vẽ nêu trên vẽ đường thẳng qua M vuông góc a tại H và đường thẳng qua M vuông góc với b tại K 

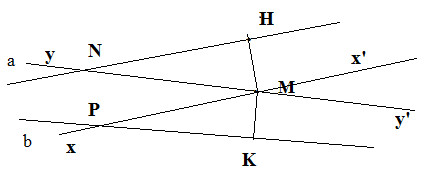
b) Vẽ đường thẳng xx’ vuông góc với MH tại M và đường thẳng yy’ vuông góc với MK tại M thì xx’ // a (vì cùng vuông góc với MH) và yy’ //b.

c) Giả sử a cắt yy’ tại N và b cắt xx’ tại P. Một số cặp góc bằng nhau là x’My’ và x’PK, HNM và MPK.

Một số cặp góc bù nhau, chẳng hạn như HNM và NMx’, KPM và PMy’.

Bài 3 trang 91 sgk toán 7 tập 2

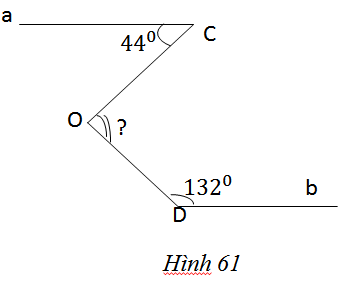
Hình 61 cho biết a//b,  \(\hat C = {44^0},\hat D = {132^0}\).

Tính số đo góc COD.

(Hướng dẫn: Vẽ đường thẳng song song với đường thẳng a và đi qua điểm O).

Hướng dẫn làm bài:

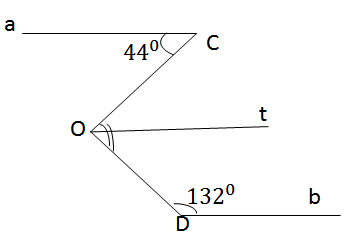
Vẽ tia Ot // a (Ca, Ot nằm ở hai nửa mp đối nhau có bờ OC).

 \(\widehat {COD} = \widehat {COt} + \widehat {DOt}\)

Mà a // Ot

=>  \(\widehat {COt} = {180^0} - \widehat {OPb}\)

(hai góc trong cùng phía)

Suy ra:  \(\widehat {tOD} = {180^0} - {132^0} = {48^0}\)

Vậy  \(\widehat {COD} = {44^0} + {48^0} = {92^0}\)

Bài 2 trang 91 sgk toán 7 tập 2

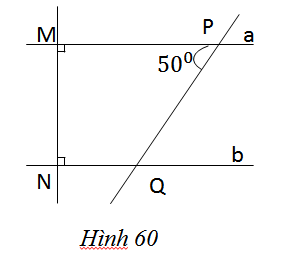
Xem hình 60.

a)Giải thích vì sao a//b.

b)Tính số đo góc NQP.

Hướng dẫn làm bài:

a) Các đường thẳng a và b cùng vuông góc với đường thẳng MN nên a//b.

b) \(\widehat {NQP} và  \widehat {QPM}\) là hai góc trong cùng phía tạo bởi đường thẳng PQ cắt hai đường thẳng song song nên chúng bù nhau.

 \(\widehat {NQP} + \widehat {QPM} = {180^0}\)

=>  \(\widehat {NQP} = {180^0} - \widehat {QPM} = {180^0} - {50^0} = {130^0}\)

Bài 4 trang 91 sgk toán 7 tập 2.

Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Đường trung trực của đoạn thẳng OA cắt Ox ở D, đường thẳng trung trực của đoạn thẳng OB cắt Oy ở E. Gọi C là giao điểm của hai đường trung trực đó. Chứng minh rằng:

a) CE = OD;                             b) CE ⊥ CD;

c) CA = CB;                             d) CA // DE;

e) Ba điểm A, B, C thẳng hàng.

Hướng dẫn làm bài:

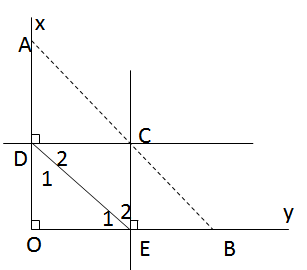
a) EC // Ox (cùng vuông góc Oy)

DC // Oy (cùng vuông góc Ox)

Do đó: \(\widehat {{D_1}} = \widehat {{E_2}}\) (So le trong)

\(\widehat {{E_1}} = \widehat {{D_2}}\) (So le trong)

Mà DE chung

=>∆CDE = ∆OED

=>CE = OD  và CD = OE

b) Vì ∆CDE = ∆OED

=>  \(\widehat {ECD} = \widehat {DOE}\)

=>CE ⊥ CD

c) Hai tam giác vuông BEC, CDA có :

CD = BE (cùng bằng OE)

CE = AD (cùng bằng OD)

=> ∆BCE = ∆CDA => CB = CA

d) Hai tam giác vuông CDA, DCE bằng nhau vì có hai cặp cạnh góc vuông tương ứng bằng nhau nên  \(\widehat {DCA} = \widehat {{D_2}}\) lại so le trong nên CA // DE.

e) Chứng minh tương tự như d suy ra CB // DE. Do đó theo tiên đề Ơ clit ta suy ra hai đường thẳng BC và CA trùng nhau hay A, B, C thẳng hàng.