Bài 5 trang 91 sgk toán 7 tập 2.

Tính số đo x trong mỗi hình 62, 63, 64:

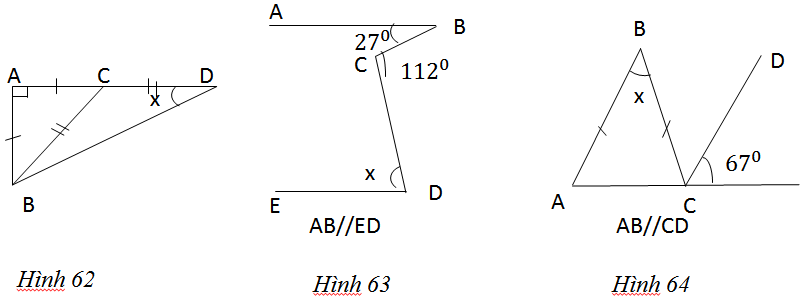
Hướng dẫn làm bài:

a)∆ABC có AC = AB,  \(\hat A = {90^0}\)nên vuông cân tại A.

=>  \(\widehat {ACB} = {45^0}\)

Mà ∆BCD cân tại C (BC = CD) có  \(\widehat {ACB}\) là góc ngoài tại C nên

\(\widehat {ACB} = 2{\rm{x}} \Rightarrow x = {1 \over 2}\widehat {ACB} = {1 \over 2}{45^0} \Rightarrow x = {22^0}30'\)

b)Vẽ tia Cx // BA (BA, Cx thuộc hai nửa mặt phẳng đối nhau có bờ BC)

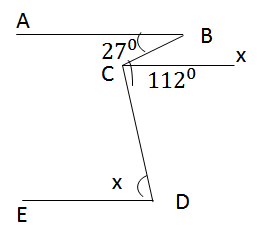
=>  \(\widehat {ABC} = \widehat {BCx} = {27^0}\)

Mà  \(\widehat {xCD} = \widehat {BCD} - \widehat {BCx} = {112^0} - {27^0} = {85^0}\)

Vì Cx //ED (cùng song song AB)

=>  \(\widehat {CDE} = \hat x = {85^0}\)

c)Vì AB // CD =>  \(\widehat {ABC} = {67^0}\) (đvi)

∆ABC cân tại A (AB = AC) nên  \(\hat x = \widehat {BAC} = {180^0} - 2\widehat {ABC} = {180^0} - {2.67^0} = {46^0}\)

Bài 6 trang 92 sgk toán 7 tập 2

Cho tam giác ADC (AD = DC) có  \(\widehat {ACD} = {31^0}\). Trên cạnh AC lấy một điểm B sao cho  \(\widehat {ABD} = {88^0}\). Từ C kẻ một tia song song với BD cắt tia AD ở E.

a)Hãy tính các góc DCE và DEC.

b)Trong tam giác CDE, cạnh nào lớn nhất? Tại sao?    

Hướng dẫn làm bài:

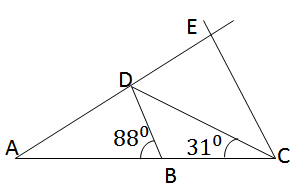
a)∆ADC cân tại D, có  \(\widehat {ADC} = {31^0} =  > \widehat {ADC} = {180^0} - 2.\hat C\)

=>  \(\widehat {ADC} = {180^0} - {62^0} = {118^0}\)

+∆ADB có  \(\hat A = {31^0},\widehat {ABD} = {88^0}\)

=>  \(\widehat {ADB} = {180^0} - \left( {{{31}^0} + {{88}^0}} \right)\)

Hay  \(\widehat {ADB} = {61^0}\)

+BD //CE

=>  \(\widehat {DEC} = \widehat {ADB} = {61^0}\) (đồng vị)

b)  \(\widehat {EDC}\) là góc ngoài ∆ADC cân tại D

=>  \(\widehat {EDC} = 2.\hat C = {62^0}\)

∆DEC có  \(\hat E = {61^0};\hat D = {62^0} =  > \widehat {DCE} = {57^0}\)

Vì  \({57^0} < {61^0} < {62^0} =  > DE < DC < CE\)
Vậy CE là cạnh lớn nhất.

Bài 7 trang 92 sgk toán 7 tập 2

Từ một điểm M trên tia phân giác của góc nhọn xOy, kẻ đường vuông góc với cạnh O (tại A), đường thẳng này cắt cạnh Oy tại B.

a)Hãy so sánh hai đoạn thẳng OA và MA.

b)Hãy so sánh hai đoạn thẳng OB và OM.

Hướng dẫn làm bài:

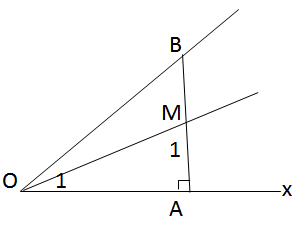
a) ∆AOM vuông tại A có

=>  \(\widehat {{O_1}} < {45^0}\) ( \(\widehat {xOy}nhn)\)

Mà  \(\widehat {{O_1}} + \widehat {{M_1}} = {90^0}\)

=>  \(\widehat {{M_1}} > {45^0} =  > \widehat {{M_1}} > \widehat {{O_1}}\)

=>OA > MA

b) ∆OMB có  \(\widehat {{M_2}}\) là góc ngoài tại M của ∆OMA

=>  \(\widehat {{M_2}} =  > \widehat {{O_1}} + {90^0} =  > \widehat {{M_2}} > {90^0}hay\widehat {{M_2}}\) là góc tù

=>OB là cạnh lớn nhất nên OB > OM

Bài 8 trang 92 sgk toán 7 tập 2

Cho tam giác ABC vuông tại A; đường phân giác BE. Kẻ EH vuông góc với BC (\(H \in BC)\). Gọi K là giao điểm của AB và HE. Chứng minh rằng:

a)∆ABE= ∆HBE.

b)BE là đường trung trực của đoạn thẳng AH.

c)EK = EC.

d)AE < EC.

Hướng dẫn làm bài:

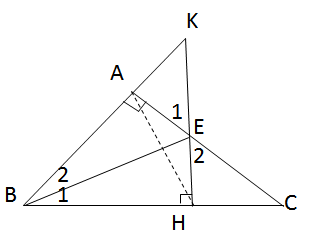
a)∆ABE = ∆HBE

Xét hai tam giác vuông ∆ABE và ∆HBE, ta có:

\(\widehat {{B_1}} = \widehat {{B_2}}\) (do BE là phân giác của góc B)

BE : cạnh huyền chung

Vậy ∆ABE = ∆HBE  (g.c.g)

b) Chứng minh BE là đường trung trực của đoạn thẳng AH.

Vì ∆ABE = ∆HBE

=>BA = BH, EA = EH

=>E, B cùng thuộc trung trực của AH nên đường thẳng EB là trung trực của AH.

c) EK = EC.

Xét 2 tam giác ∆AEK và ∆HEC , ta có: \(\widehat H = \widehat A = {90^0}\)

EA = EH (chứng minh trên)

\(\widehat {{E_2}} = \widehat {{E_1}}\) (đối đỉnh)

Vậy ∆AEK = ∆HEC => EK = EC (đpcm)

Trong tam giác vuông AEK ta có:

AE < EK (cạnh huyền lớn hơn cạnh góc vuông)

Mà EC = EK. Suy ra EC < EK (đpcm)