Bài 36 trang 72 sgk toán lớp 7- tập 2
Cho tam giác DEF, điểm I nằm trong tam giác và cách đều ba cạnh của nó. Chứng minh I là điểm chung của ba đường phân giác của tam giác DEF.
Hướng dẫn:
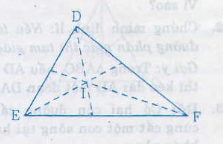
I nằm trong ∆DEF và cách đều ba cạnh của tam giác nên I lần lượt thuộc phân giác của các góc \(\widehat{D}\), \(\widehat{E}\), \(\widehat{F}\)
Vậy I là điểm chung của ba đường phân giác của tam giác DEF
Bài 37 trang 72 sgk toán lớp 7- tập 2
Nêu cách vẽ điểm K ở trong tam giác MNP mà các khoảng cách từ K đến ba cạnh của tam giác đó bằng nhau. Vẽ hình minh họa.
Hướng dẫn:
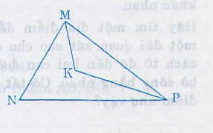
Vẽ điểm K ở trong tam giác MNP mà các khoảng cách từ K đến ba cạnh của tam giác đó bằng nhau tức là K là giao điểm của các đường phân giác trong tam giác MNP
Vì vậy ta chỉ cần vẽ phân giác của hai trong ba góc của ∆MNP
Bài 38 trang 73 sgk toán lớp 7- tập 2
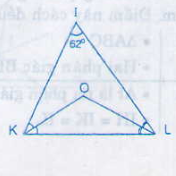
Cho hình bên
a) Tính góc KOL
b) Kẻ tia IO, hãy tính góc KIO
c) Điểm O có cách đều ba cạnh của tam giác IKL không? Tại sao?
Hướng dẫn:
a) ∆KIL có \(\widehat{I}\) = 620
nên \(\widehat{IKL}+ \widehat{ILK}\) = 1180
Vì KO và LO là phân giác \(\widehat{IKL}\), \(\widehat{ILK}\)
nên \(\widehat{OKL}+ \widehat{OLK}\)= \(\frac{1}{2}\)(\(\widehat{IKL}+ \widehat{ILK}\))
=> \(\widehat{OKL}+ \widehat{OLK}\) = \(\frac{1}{2}\) 1180
\(\widehat{OKL}+ \widehat{OLK}\) = 590
∆KOL có \(\widehat{OKL}+ \widehat{OLK}\) = 590
nên \(\widehat{KOL}\) = 1800 – 590 = 1210

c) Vì O là giao điểm của hai đường phân giác của \(\widehat{K}\) và \(\widehat{L}\) nên O cách đều ba cạnh của tam giác IKL
Bài 39 trang 73 sgk toán lớp 7- tập 2
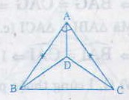
Cho hình bên.
a) chứng minh ∆ABD = ∆ACD
b) So sánh góc DBC với góc DCB
Hướng dẫn:
a) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
\(\widehat{BAD}= \widehat{CAD}\)
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=> \(\widehat{DBC}= \widehat{DCB}\)
Giaibaitap.me
Giải bài tập trang 72, 73 bài 6 Tính chất ba đường phân giác của tam giác Sách giáo khoa (SGK) Toán 7. Câu 40: Chứng minh ba điểm A, G, I thẳng hàng...
Giải bài tập trang 76 bài 7 Tính chất đường trung trực của một đoạn thẳng Sách giáo khoa (SGK) Toán 7. Câu 44: Hỏi độ dài MB bằng bao nhiêu...
Giải bài tập trang 77 bài 7 Tính chất đường trung trực của một đoạn thẳng Sách giáo khoa (SGK) Toán 7. Câu 48: Hai điểm M và N cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng xy...
Giải bài tập trang 79, 80 bài 8 Tính chất ba đường trung trực của tam giác Sách giáo khoa (SGK) Toán 7. Câu 52: Chứng minh định lí: Nếu tam giác có một đường trung tuyến...
