Câu 3.5 trang 41 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Chứng minh rằng trong một đường tròn, đường kính là dây lớn nhất.
Giải
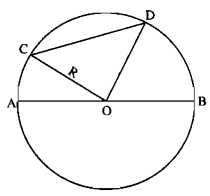
Giả sử CD là một dây của đường tròn bán kính R và AB là một đường kính của nó. Ta có:
- Nếu C, O, D không thẳng hàng thì trong tam giác COD có
CD < OC + OD = 2R = AB.
- Nếu C, O, D thằng hàng thì
CD = OC + OD = 2R = AB
Vậy trong mọi trường hợp ta luôn có đường kính là dây lớn nhất.
Câu 3.6 trang 41 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Chứng minh “Bất đẳng thức tam giác mở rộng ”: Với ba điểm A, B, C bất kỳ, ta có
AB + AC ≥ BC
Giải
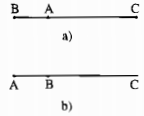
- Nếu A, B, C không thẳng hàng thì trong tam giác ABC ta có AB + AC > BC
- Nếu A, B, C thẳng hàng và A ở giữa B và C hoặc trùng B, C thì AB + AC = BC
Vậy với ba điểm A, B, C bất kỳ ta luôn có AB + AC ≥ BC
Câu 3.7 trang 41 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho đường thẳng d và hai điểm A, B nằm cùng một phía của d và AB không song song với d. Một điểm M di động trên d. Tìm vị trí của M sao cho \(\left| {MA - MB} \right|\) là lớn nhất
Giải
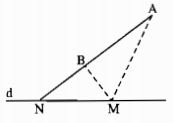
Vì AB không song song với d nên AB cắt d tại N.
Với điểm M bất kỳ thuộc d mà M không trùng với N thì ta có tam giác MAB.
Do đó
\(\left| {MA - MB} \right| < AB\)
Khi M ≡ N thì
\(\left| {MA - MB} \right| = AB\)
Vậy \(\left| {MA - MB} \right|\) lớn nhất là bằng AB, khi đó M ≡ N là giao điểm của hai đường thẳng d và AB.
Giaibaitap.me
Giải bài tập trang 41 bài 3 quan hệ giữa ba cạnh của một tam giác, bất đẳng thức tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 3.1: Bộ ba nào sau đây không thể là số đo ba cạnh của một tam giác?...
Giải bài tập trang 42 bài 4 tính chất ba đường trung tuyến của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 31: Cho hình bên. Điền vào chỗ trống...
Giải bài tập trang 42, 43 bài 4 tính chất ba đường trung tuyến của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 35: Tam giác ABC có BC = 10cm, các đường trung tuyến BD và CE. Chứng minh rằng BD + CE < 15cm....
Giải bài tập trang 43, 44 bài 4 tính chất ba đường trung tuyến của tam giác Sách Bài Tập (SBT) Toán lớp 7 tập 2. Câu 4.1: Cho tam giác ABC. Trên đường trung tuyến AM của tam giác đó, lấy hai điểm...
