Câu 31 trang 110 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Tính số đo x của góc AOB ở hình dưới, cho biết a // b.
Giải
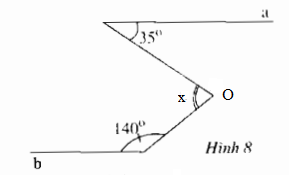
Qua O kẻ đường thẳng c // a
Vì a // b nên c // b
\(\widehat A = \widehat {{O_1}}\) (hai góc so le trong)
Mà \(\widehat A = 35^\circ \) nên \(\widehat {{O_1}} = 35^\circ \)
Vì \(\widehat {{O_2}}\) và \(\widehat B\) là hai góc trong cùng phía của hai đường thẳng song song nên \(\widehat {{O_2}} + \widehat B = 180^\circ \)
\(\eqalign{
& \Rightarrow \widehat {{O_2}} = 180^\circ - \widehat B \cr
& \Rightarrow \widehat {{O_2}} = 180^\circ - 140^\circ = 40^\circ \cr
& x = \widehat {AOB} = \widehat {{O_1}} + \widehat {{O_2}} = 35^\circ + 40^\circ = 75^\circ \cr}\)
Câu 32 trang 110 Sách Bài Tập (SBT) Toán lớp 7 tập 1
a) Dùng êke vẽ hai đường thẳng a, b cùng vuông góc với đường thẳng c.
b) Tại sao a // b?
c) Vẽ đường thẳng d cắt a, b lần lượt tại C, D. Đánh số các góc đỉnh C, đỉnh D rồi viết tên các cặp góc bằng nhau.
Giải
a) Hình vẽ:
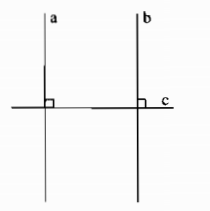
b) c cắt a và b, trong các góc tạo thành có cặp góc đồng vị bằng nhau và bằng 90° nên a // b.
Câu 33 trang 110 Sách Bài Tập (SBT) Toán lớp 7 tập 1
a) Vẽ a // b và \(c \bot a\)
b) Quan sát xem c có vuông góc với b hay không.
c) Lí luận tại sao nếu a // b và \(c \bot a\) thì \(c \bot b\)
Giải
a) Hình vẽ:
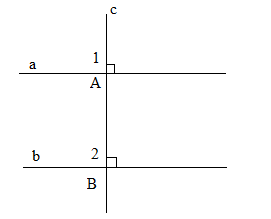
b) Dùng êke ta thấy b vuông góc với c
c) Vì a // b nên c cắt a tại A thì c cắt b tại B
Ta có: \(a \bot c \Rightarrow \widehat {{A_1}} = 90^\circ \); \(\widehat {{A_1}}\) và \(\widehat {{B_2}}\) là cặp góc đồng vị.
Suy ra: \(\widehat {{B_2}} = \widehat {{A_1}} = 90^\circ \)
Vậy: \(b \bot c\).
Câu 34 trang 110 Sách Bài Tập (SBT) Toán lớp 7 tập 1
a) Vẽ ba đường thẳng a, b, c sao cho b // a và c // a.
b) Kiểm tra xem b và c có song song với nhau không.
c) Lý luận tại sao nếu b //a và c // a thì b // c?
Giải
a) Hình vẽ:
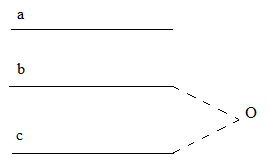
b) b // c
c) Giả sử b và c không song song nên b cắt c tại điểm O nào đó.
Ta có \(O \notin a\) vì O ∈ b và b // a
Vậy qua điểm O kẻ được 2 đường thẳng b và c cùng song song với đường thẳng a, điều đó trái với tiên đề Ơ clít.
Vậy b // c.
Giaibaitap.me
Giải bài tập trang 110 bài 66 từ vuông góc đến song song Sách Bài Tập Toán lớp 7 tập 1. Câu 35: Vẽ ba đường thẳng a, b, c sao cho a // b // c....
Giải bài tập trang 111, 112 bài 7 định lý Sách Bài Tập Toán lớp 7 tập 1. Câu 39: Vẽ hình và viết giả thiết, kết luận của các định lí sau...
Giải bài tập trang 112, 113 bài 7 định lý Sách Bài Tập Toán lớp 7 tập 1. Câu 42: Điền vào chỗ (…) để chứng minh bài toán sau...
Giải bài tập trang 113, 114 bài ôn tập chương 1 đường thẳng vuông góc, đường thẳng song song Sách Bài Tập Toán lớp 7 tập 1. Câu 45: Vẽ hình theo trình tự sau...
