Bài 31 trang 70 sgk toán lớp 7- tập 2
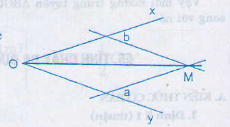
Hình vẽ bên cho biết cách vẽ tia phân giác của góc xOy bằng thước hai lề :
- Áp một lề của thước vào cạnh Ox, kẻ đường thẳng a theo lề kia.
- Làm tương tự với cạnh Oy, ta kẻ được đường thẳng b.
-Gọi M là giao điểm của a và b, ta có OM là tia phân giác của góc xOy
Hãy chứng minh tia OM được vẽ như vậy đúng là tia phân giác của góc xOy.
( gợi ý : Dựa vào bài tập 12 chứng minh các khoảng cách từ M đến Ox và đến Oy bằng nhau (do cùng bằng khoảng cách hai lề của chiếc thước) rồi áp dụng định lí 2).
Hướng dẫn :
Theo cách vẽ thì M cách đều hai cạnh Ox, Oy (cùng bằng khoảng cách 2 lề của chiếc thước
Vì M cách đều Ox, Oy nên theo định lí đảo M thuộc phân giác của \(\widehat{xOy}\) hay OM là phân giác của \(\widehat{xOy}\).
Bài 32 trang 70 sgk toán lớp 7- tập 2
32. Cho tam giác ABC. Chứng minh rằng giao điểm của hai tia phân giác của hai góc ngoài B1 và C1 nằm trên tia phân giác của góc A.

Hướng dẫn :
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)
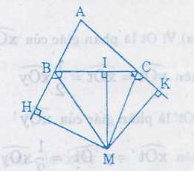
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của góc \(\widehat{BAC}\)
Bài 33 trang 70 sgk toán lớp 7- tập 2
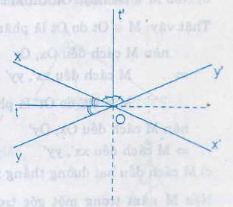
33. Cho hai đường thẳng xx’, yy’cắt nhau tại O
a) Chứng minh rằng hai tia phân giác Ot, Ot’ của một cặp góc kề bù tạo thành một góc vuông.
b) Chứng minh rằng : Nếu M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot’ thì M cách đều hai đường thẳng xx’, yy’
c) Chứng minh rằng : Nếu M cách đều hai đường thẳng xx’, yy’ thì M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot’
d) Khi M ≡ O thì khoảng cách từ M đến xx’ và yy’ bằng bao nhiêu ?
e) Em có nhận xét gì về tập hợp các điểm cách đều hai đường thẳng cắt nhau xx’ và yy’
Hướng dẫn:
a) Vì Ot là phân giác của \(\widehat{xOy}\)
nên \(\widehat{yOt}\) = \(\widehat{xOt}\) = \(\frac{1}{2}\)\(\widehat{xOy}\)
Ot' là phân giác của \(\widehat{xOy'}\)
nên \(\widehat{xOt'}\) = \(\widehat{y'Ot'}\) = \(\frac{1}{2}\)\(\widehat{xOy'}\)
=> \(\widehat{xOt}\) + \(\widehat{xOt'}\) = \(\frac{1}{2}\)\(\widehat{xOy}\) + \(\frac{1}{2}\)\(\widehat{xOy'}\) = \(\frac{1}{2}\)(\(\widehat{xOy}\) + \(\widehat{xOy'}\))
mà (\(\widehat{xOy}\) + \(\widehat{xOy'}\)) = 1800 (2 góc kề bù)
=> \(\widehat{xOt}\) + \(\widehat{xOt'}\) = \(\frac{1}{2}\)1800 = 900
Vậy hai tia phân giác của hai góc kề bù tạo thành một góc vuông
b) Nếu M thuộc Ot hoặc Ot' thì M cách đều hai đường thẳng xx' và yy'
Thật vậy: M ε Ot do Ot là phân giác của \(\widehat{xOy}\) nên M cách đều Ox, Oy
=> M cách đều xx',yy'
M ε Ot'do Ot' là phân giác của \(\widehat{xOy'}\) nên M cách đều xx', yy'
=> M cách đều xx',yy'
c) M cách đều hai đường thẳng xx', yy'
Nếu M nằm trong một góc trong bốn góc \(\widehat{xOy}\), \(\widehat{xOy'}\), \(\widehat{x'Oy'}\), \(\widehat{x'Oy}\) thì M phải thuộc phân giác của góc ây tức M phải thuộc Ot hoặc Ot'
d) Khi M ≡ O thì khoảng cách từ M đến xx', yy' bằng 0
e) Từ các câu trên ta có nhận xét: Tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' thuộc hai đường thẳng vuông góc nhau lần lượt là phân giác của các góc tạo bởi hai đường thẳng cắt nhau đó.
Bài 34 trang 71 sgk toán lớp 7- tập 2
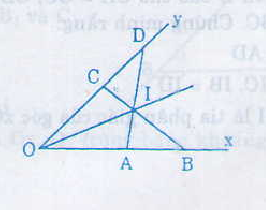
34.Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC, OB = OD. Gọi I là giao điểm của hai đoạn thẳng AD và BC. Chứng minh rằng :
a) BC = AD
b) IA = IC, IB = ID
c) Tia OI là tia phân giác của góc xOy
Hướng dẫn:
a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
\(\widehat{xOy}\) là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC
b) ∆AOD = ∆COB => \(\widehat{AOD} = \widehat{OCB}\)
=> \(\widehat{BAI} = \widehat{DCI}\) (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
\(\widehat{DCI} = \widehat{ABI}\) ( ∆AOD = ∆COB)
\(\widehat{BAI} = \widehat{DCI}\) (chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=> \(\widehat{COI} = \widehat{AOI}\)
=> OI là phân giác của \(\widehat{xOy}\)
Bài 35 trang 71 sgk toán lớp 7- tập 2
35. Có mảnh sắt phẳng hình dạng một góc (hình dưới) và một chiếc thước có chia khoảng. làm thế nào để vẽ được tia phân giác của góc này?
Hướng dẫn:

+ Trên cạnh thứ nhất lấy hai điểm phân biệt A; B trên cạnh thứ hai lấy hai điểm C; D sao cho khoảng cách từ C; D đến đỉnh của góc lần lượt bằng khoảng cách từ đỉnh của góc với A, B
+ Xác định giao điểm I của BC và AD; tia vẽ từ đỉnh của góc qua I chính là tia phân giác của góc đó.
+ Phần chứng minh tương tự như bài 34
Giaibaitap.me
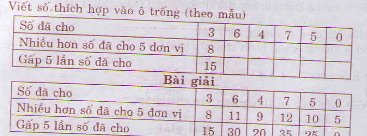
Giải bài tập trang 72, 73 bài 6 Tính chất ba đường phân giác của tam giác Sách giáo khoa (SGK) Toán 7. Câu 36: Cho tam giác DEF, điểm I nằm trong tam giác...
Giải bài tập trang 72, 73 bài 6 Tính chất ba đường phân giác của tam giác Sách giáo khoa (SGK) Toán 7. Câu 40: Chứng minh ba điểm A, G, I thẳng hàng...
Giải bài tập trang 76 bài 7 Tính chất đường trung trực của một đoạn thẳng Sách giáo khoa (SGK) Toán 7. Câu 44: Hỏi độ dài MB bằng bao nhiêu...
Giải bài tập trang 77 bài 7 Tính chất đường trung trực của một đoạn thẳng Sách giáo khoa (SGK) Toán 7. Câu 48: Hai điểm M và N cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng xy...
