Bài 28 trang 67 sgk toán lớp 7- tập 2

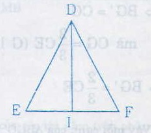
28.Cho tam giác DEF cân tại D với đường trung tuyến DI

a) Chứng minh ∆DEI  = ∆DFI

b) Các góc DIE và góc DIF là những góc gì?

c) Biết DE = DF = 13cm, EF = 10cm, hãy tính độ dài đường trung tuyến DI.

Hướng dẫn:

a) ∆DEI  = ∆DFI có:

DI là cạnh chung

DE = DF ( ∆DEF cân)

IE = IF (DI là trung tuyến)

=>  ∆DEI  = ∆DFI (c.c.c)

b) Vì  ∆DEI  = ∆DFI => \(\widehat{DIE} =\widehat{DIF}\)

mà \(\widehat{DIE} +\widehat{DIF}\) = 180⁰ ( kề bù)

nên \(\widehat{DIE} =\widehat{DIF}\) = 90⁰ 

c) I là trung điểm của  EF nên IE = IF = 5cm

∆DEI  vuông tại I => DI² = DE² – EI² (định lí pytago)

=> DI² = 13² – 5² = 144

=> DI = 12

Bài 29 trang 67 sgk toán lớp 7- tập 2

29. Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng:

GA =GB = GC.

Hướng dẫn:

Gọi M, N, E là giao điểm của AG, BG, CG với BC, CA, AB.

Vì G là trọng tâm của ∆ABC nên

GA = \(\frac{2}{3}\)AM; GB = \(\frac{2}{3}\)BN;  GC = \(\frac{2}{3}\)CE (1)

Vì ∆ABC đều nên ba đường trung tuyến ứng với ba cạnh BC, CA, AB bằng nhau

=> AM = BN = CE (2)

Từ (1), (2)  => GA = GB = GC

Bài 30 trang 67 sgk toán 7 tập 2

Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’.

a)So sánh các cạnh của tam giác BGG’ với các đường trung tuyến của tam giác ABC.

b)So sánh các đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.

Hướng dẫn làm bài:

a)So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC

BG cắt AC tại N

CG cắt AB tại E

G là trọng tâm của ∆ABC

=>  \(GA = {2 \over 3}AM\)

Mà GA = GG’ (G là trung điểm của AG’)

=>  \(GG' = {2 \over 3}AM\)

Vì G là trọng tâm của ∆ABC =>  \(GB = {2 \over 3}BN\)

Mặt khác :  

M là trung điểm \(\left. {\matrix{{GM = {1 \over 2}AG\left( {TT} \right)} \cr {AG = GG'\left( {Gt} \right)} \cr} } \right\} = > GM = {1 \over 2}GG'\)

Do đó ∆GMC=∆G’MB vì  \(\left\{ {\matrix{{GM = MG'}  \cr {MB = MC}  \cr {\widehat {GMC} = \widehat {G'MB}}  \cr } } \right.\)

=> \({\matrix{{BG' = CG} \cr {{\rm{ }}CG = {2 \over 3}CE} \cr} }\) (G là trọng tâm tam giác ABC) 

\(=  > BG' = {2 \over 3}CE\)

Vậy mỗi cạnh của ∆BGG’ bằng  \({2 \over 3}\) đường trung tuyến của ∆ABC

b)So sánh các đường trung tuyến của ∆BGG’ với cạnh ∆ABC.

-Ta có: BM là đường trung tuyến ∆BGG’

Mà M là trung điểm của BC nên  \(BM = {1 \over 2}BC\)

Vì \({IG = {1 \over 2}BG}\) (Vì I là trung điểm BG)

\({GN = {1 \over 2}BG}\) (G là trọng tâm)

 => IG = GN

Do đó ∆IGG’=∆NGA (c.g.c) =>  \(IG' = AN =  > IG' = {{AC} \over 2}\)

-Gọi K là trung điểm BG => GK là trung điểm ∆BGG’

Vì \({GE = {1 \over 2}GC}\) (G là trọng tâm tam giác ABC)

BG' = GC (Chứng minh trên)

\(=  > GE = {1 \over 2}BG\)

Mà K là trung điểm BG’ =>KG’ = EG

Vì ∆GMC = ∆G’MB (chứng minh trên)

=>  \(\widehat {GCM} = \widehat {G'BM}\) (So le trong)

=>CE // BG’ =>  \(\widehat {AGE} = \widehat {AG'B}\) (đồng vị)

Do đó ∆AGE = ∆GG’K (c.g.c) =>AE = GK

Mà  \(AE = {1 \over 2}AB \Rightarrow GK = {1 \over 2}AB\)

Vậy mỗi đường trung tuyến ∆BGG’ bằng một nửa cạnh của tam giác ABC song song với nó.

Giaibaitap.me