Bài 82 trang 41 sgk toán 7 - tập 1
Theo mẫu: Vì \(2^2= 4\) nên \(\sqrt4 = 2\), hãy hoàn thành bài tập sau:
a) \(5^2 ….\) nên \(.... = 5\);
b) Vì \(...= 49\) nên \(... = 7\);
c) Vì \(1...= 1\) nên \(\sqrt1 = ...\);
d) Vì \({\left( {{2 \over 3}} \right)^2}...\) nên\( ... = ...\)
Giải
a) Vì \(5^2= 25\) nên \(\sqrt{25} = 5\)
b) Vì \(7^2= 49\) nên \(\sqrt{49} = 7\)
c) Vì \(1^2= 1\) nên \(\sqrt1 = 1\)
d) Vì \({\left( {{2 \over 3}} \right)^2} = {4 \over 9}\) = nên \(\sqrt {{4 \over 9}} = {2 \over 3}\)
Bài 83 trang 41 sgk toán 7 - tập 1
Ta có \(\sqrt{25}=5; -\sqrt{25}=-5; \sqrt{(-5)^{2}}=\sqrt{25}=5.\)
Theo mẫu trên, hãy tính:
a) \(\sqrt{36}\);
b) \(-\sqrt{16}\);
c) \(\sqrt{\frac{9}{25}};\)
d) \(\sqrt{3^{2}};\)
e) \(\sqrt{(-3)^{2}}.\)
Giải:
a) \(\sqrt{36}=6\);
b) \(-\sqrt{16}=-4\);
c) \(\sqrt{\frac{9}{25}}=\frac{3}{5}\);
d) \(\sqrt{3^{2}}=3\);
e) \(\sqrt{(-3)^{2}}=\sqrt{9}=3.\)
Bài 84 trang 41 sgk toán 7 - tập 1
Nếu \(\sqrt{x}=2\) thì \(x^{2}\) bằng:
A) 2;
B) 4;
C) 8;
D) 16.
Hãy chọn câu trả lời đúng.
Hướng dẫn giải:
Ta có: \(\sqrt{x}=2\Rightarrow x=2^{2}=4\)
Do đó \(x^{2}=4^{2}=16.\)
Vậy chọn D) \(16\).
Bài 85 trang 42 sgk toán 7 - tập 1
Bài 85. Điền số thích hợp vào ô trống

Hướng dẫn giải:
Định nghĩa: Căn bậc hai của một số a không âm là số \(x\) sao cho \({x^2} = a\)
Các số được điền vào là các số có khoanh tròn trong bảng dưới đây:
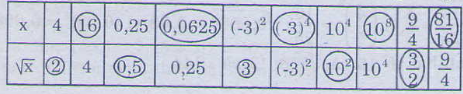 .
.
Bài 86 trang 42 sgk toán 7 - tập 1
Bài 86. Sử dụng máy tính bỏ túi.
Nút dấu căn bậc hai: ![]()

Dùng máy tính bỏ túi để tính:
\(\sqrt{3783025};\sqrt{1125,45}; \sqrt{\frac{0,3+1,2}{0,7}};\frac{\sqrt{6,4}}{1,2}.\)
Hướng dẫn giải:

Chú ý: Trong các kết quả trên, hai kết quả đầu là căn bậc hai đúng, hai kết quả cuối là căn bậc hai gần đúng chính xác đến 6 chữ số thập phân (được làm tròn đến chữ số thập phân thứ sáu)
Giaibaitap.me
Giải bài tập trang 44, 45 bài 12 số thực Sách giáo khoa (SGK) Toán 7. Câu 87: Điền các dấu...
Giải bài tập trang 45 bài 12 số thực Sách giáo khoa (SGK) Toán 7. Câu 91: Điền chữ số thích hợp vào ô vuông...
Giải bài tập trang 48, 49 bài Ôn tập chương I - Số hữu tỉ. Số thực Sách giáo khoa (SGK) Toán 7. Câu 96: Thực hiện phép tính (bằng cách hợp lí nếu có thể...
Giải bài tập trang 49, 50 bài Ôn tập chương I - Số hữu tỉ. Số thực Sách giáo khoa (SGK) Toán 7. Câu 101: Tìm x...
