Câu 8.1 trang 50 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác cân (không đều) ABC có AB = AC. Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. Khi đó khẳng định nào sau đây là đúng?

\(\left( A \right)OA > OB\)

\(\left( B \right)\widehat {AOB} > \widehat {AOC}\)

\(\left( C \right)AO \bot BC\)

(D)O cách đều ba cạnh của tam giác ABC

Giải

Vì O thuộc đường trung trực của cạnh AB nên OA = OB. Vì ba đường trung trực của một tam giác đồng quy nên OA là đường trung trực của BC, do đó \(AO \bot BC\). Vì tam giác ABC cân tại A nên đường trung trực AO đồng thời là đường phân giác của góc A, do đó ∆AOB = ∆AOC, suy ra \(\widehat {AOB} = \widehat {AOC}\). Do đó tam giác ABC cân tại A nhưng không là tam giác đều nên O không là giao điểm của ba đường phân giác của tam giác ABC. Vậy O không cách đều ba cạnh của tam giác ABC.

Đáp số \(\left( C \right)AO \bot BC\).

Câu 8.2 trang 50 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC vuông tại A. Gọi P, Q, R lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi O là giao điểm của ba đường phân giác. Khi đó, tâm đường trong ngoại tiếp tam giác ABC là điểm:

(A) O                   (B) P;

(C) Q;                 (D) R.

Hãy chọn phương án đúng.

Giải

Chọn đáp án (D) R.

Câu 8.3 trang 50 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC có Â = 100°. Các đường trung trực của AB và AC lần lượt cắt BC ở E và F. Tính \(\widehat {{\rm{EAF}}}\).

Giải

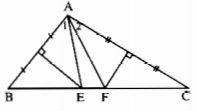
Vì E thuộc đường trung trực của đoạn thẳng AB nên EA = EB, hay tam giác EAB cân tại đỉnh E. Suy ra \(\widehat B = \widehat {{A_1}}\). Tương tự, có \(\widehat C = \widehat {{A_2}}\). Ta có: 

$$\widehat {{\rm{EAF}}} = \widehat A - \left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = \widehat A - \left( {\widehat B + \widehat C} \right)$$

Mặt khác

$$\widehat B + \widehat C = 180^\circ  - \widehat A = 180^\circ  - 100^\circ  = 80^\circ $$

Do đó \(\widehat {{\rm{EAF}}} = 100^\circ  - 80^\circ  = 20^\circ \)

Câu 8.4 trang 50 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC có góc A là góc tù. Các đường trung trực của AB; AC cắt nhau tại O và lần lượt cắt BC tại M, N. Chứng minh rằng AO là tia  phân giác của góc MAN.

Giải

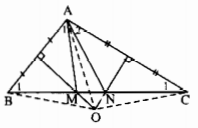
Theo bài 8.3 ta đã có \(\widehat {{A_1}} = \widehat {{B_1}},\widehat {{A_2}} = \widehat {{C_1}}\)         (1)

Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra \(\widehat {OAB} = \widehat {OBA},\)\(\widehat {OAC} = \widehat {OC{\rm{A}}}\), \(\widehat {OBC} = \widehat {OCB}\). Kết hợp với (1) \(\widehat {OBM} = \widehat {OAM},\widehat {OCN} = \widehat {OAN}\) hay \(\widehat {OAM} = \widehat {OBC} = \widehat {OCB} = \widehat {OAN}\). Vậy OA là tia phân giác góc MAN.

Giaibaitap.me