Câu 57 trang 18 Sách Bài Tập (SBT) Toán 7 tập 1
Chứng minh các đẳng thức sau:
a) \({12^8}{.9^{12}} = {18^{16}}\) b) \({75^{20}} = {45^{10}}{.5^{30}}\)
Giải
a) \({12^8}{.9^{12}} = {18^{16}}\)
Ta có: \({12^8}{.9^{12}} = {\left( {4.3} \right)^8}{.9^{12}} = {4^8}{.3^8}{.9^{12}} = {\left( {{2^2}} \right)^8}.{\left( {{3^2}} \right)^4}{.9^{12}}\)
\( = {2^{16}}{.9^4}{.9^{12}} = {2^{16}}{.9^{16}} = {\left( {2.9} \right)^{16}} = {18^{16}}\)
Vế trái bằng vế phải nên đẳng thức được chứng minh.
b) \({75^{20}} = {45^{10}}{.5^{30}}\)
Ta có: \({45^{10}}{.5^{30}} = {\left( {9.5} \right)^{10}}{.5^{30}} = {9^{10}}{.5^{10}}{.5^{30}} = {\left( {{3^2}} \right)^{10}}{.5^{40}}\)
\( = {3^{20}}.{\left( {{5^2}} \right)^{20}} = {3^{20}}{.25^{20}} = {\left( {3.25} \right)^{20}} = {75^{20}}\)
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Câu 58 trang 18 Sách Bài Tập (SBT) Toán 7 tập 1
Hình vuông dưới đây có tính chất: mỗi ô ghi một lũy thừa của 10; tích các số trong mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau. Hãy điền các số còn thiếu vào các ô trống:
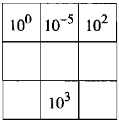
Giải
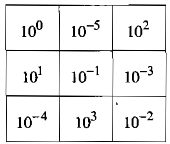
Câu 59 trang 18 Sách Bài Tập (SBT) Toán 7 tập 1
Chứng minh rằng \({10^6} - {5^7}\) chia hết cho 59.
Giải
\({10^6} - {5^7} = {\left( {2.5} \right)^6} - {5^6}.5 = {2^6}{.5^6} - {5^6}.5 \)
\(= {5^6}.\left( {{2^6} - 5} \right) = {5^6}.59\) \( \vdots\) \( 59\)
Giaibaitap.me
Giải bài tập trang 19 bài 6 lũy thừa của một số hữu tỉ (tiếp theo) Sách Bài Tập Toán lớp 7 tập 1. Câu 6.5: Tìm chữ số hàng đơn vị của số b...
Giải bài tập trang 19 bài 7 tỷ lệ thức Sách Bài Tập Toán lớp 7 tập 1. Câu 60: Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên...
Giải bài tập trang 21 bài 7 tỷ lệ thức Sách Bài Tập Toán lớp 7 tập 1. Câu 64: Lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau...
Giải bài tập trang 21 bài 7 tỷ lệ thức Sách Bài Tập Toán lớp 7 tập 1. Câu 68: Hãy lập tất cả các tỉ lệ thức từ bốn trong năm số sau đây...
