Bài 50 trang 127 - Sách giáo khoa toán 7 tập 1
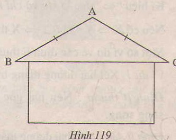
Hai thanh AB và AC vì kèo một mái nhà thường bằng nhau(h.119)
và thường tạo với nhau một góc bằng:
a) 1450 nếu là nhà tôn;
b) 1000 nếu là nhà ngói;
Tính góc BAC trong từng trường hợp.
Giải:
Ta có: AB=AC nên tam giác ABC cân ở A, Do đó \(\widehat{B}\)=\(\widehat{C}\)
a) Trong ∆ABC có \(\widehat{A}\)+\(\widehat{B}\)+\(\widehat{C}\)= 1800
mà \(\widehat{B}\)= \(\widehat{C}\) nên \(\widehat{A}\)+2\(\widehat{B}\)= 1800
2\(\widehat{B}\)= 1800-\(\widehat{A}\)=1800-1450
=> \(\widehat{B}\)=22,50
vậy \(\widehat{ABC}\)=22,50
b) tương tự với \(\widehat{A}\)=1000
vậy \(\widehat{ABC}\)=400
Bài 51 trang 128 - Sách giáo khoa toán 7 tập 1
Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD=AE.
a) So sánh \(\widehat{ABD}\) và \(\widehat{ACE}\).
b ) Gọi I là giao điểm BD và CE. Tam giác IBC là tam giác gì? Vì sao?
Giải:
∆ABD và ∆ACE có:
AB=AC(gt)
\(\widehat{A}\) góc chung.
AD=AE(gt)
Nên ∆ABD=∆ACE(c.g.c)
Suy ra: \(\widehat{ABD}\)=\(\widehat{ACE}\).
Tức là \(\widehat{B_{1}}\) =\(\widehat{C_{1}}\).
b) Ta có \(\widehat{B}\)=\(\widehat{C}\) mà \(\widehat{B_{1}}\) =\(\widehat{C_{1}}\) suy ra \(\widehat{B_{2}}\)=\(\widehat{C_{2}}\).
Vậy ∆IBC cân tại I.
Bài 52 trang 128 - Sách giáo khoa toán 7 tập 1
Cho góc xOy có số đo \(120^0\), điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox (B thuộc Ox), kẻ AC vuông góc với Oy (C thuộc Oy). Tam giác ABC là tam giác gì ? Vì sao?
Giải
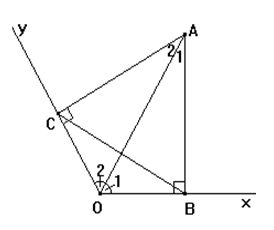
Tam giác ACO vuông tại C
Tam giác ABO vuông tại B
Xét hai tam giác vuông ACO và ABO có:
+) \(\widehat{O_{1}}=\widehat{O_{2}}\) (Vì OA là tia phân giác góc xOy)
+) AO chung
Suy ra \(∆ACO=∆ABO\) (cạnh huyền-góc nhọn)
Suy ra \(AC=AB\) (hai cạnh tương ứng)
\(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng)
\(\widehat {{O_1}} = {1 \over 2}\widehat {xOy} = {1 \over 2}{.120^0} = {60^0}\) (Vì OA là tia phân giác góc xOy)
Áp dụng định lí tổng ba góc trong một tam giác vào \(\Delta OBA\) ta có:
\(\eqalign{
& \widehat {{O_1}} + \widehat B + \widehat {{A_1}} = {180^0} \cr
& \Rightarrow \widehat {{A_1}} = {180^0} - \widehat {{O_1}} - \widehat B = {180^0} - {60^0} - {90^0} = {30^0} \cr} \)
Do đó: \(\widehat {{A_1}} = \widehat {{A_2}} = {30^0}\)
Hay \(\widehat {BAC} = \widehat {{A_1}} + \widehat {{A_2}} = {60^0}\)
Vây \(∆ABC\) có \(AC=AB\) và \(\widehat {BAC}= {60^0}\) nên là tam giác đều
Giaibaitap.me
Giải bài tập trang 131 bài 7 Định lí Pi-ta-go Sách giáo khoa (SGK) Toán 7. Câu 53: Tìm độ dài x trên hình 127...
Giải bài tập trang 131, 132, 133 bài 7 Định lí Pi-ta-go Sách giáo khoa (SGK) Toán 7. Câu 57: Cho bài toán "Tam giác ABC có AB = 8cm, AC=17cm, BC =15cm...
Giải bài tập trang 133 bài 7 Định lí Pi-ta-go Sách giáo khoa (SGK) Toán 7. Câu 60: Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC...
Giải bài tập trang 136, 137 bài 8 Các trường hợp bằng nhau của tam giác vuông Sách giáo khoa (SGK) Toán 7. Câu 63: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC(H thuộc BC)...
