Bài 41 trang 124 - Sách giáo khoa toán 7 tập 1

Cho tam giác \(ABC\), các tia phân giác của các góc \(B\) và \(C\) cắt nhau ở \(I\). Vẽ \(ID\) \(\perp\) \(AB\) (\(D\) nằm trên\( AB\)), \(IE\) \(\perp\) \(BC\) (\(E\) thuộc \(BC\) ), \(IF\) vuông góc với \(AC\) (\(F\) thuộc \(AC\))                                   

CMR: \(ID=IE=IF\).

Giải:

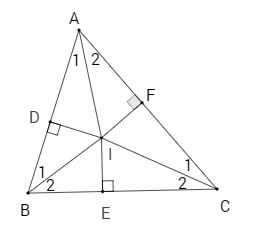
Xét hai tam giác vuông \(BID\) và \(BIE\) có:

+) \(BI\) là cạnh chung

+) \(\widehat{B_{1}}=\widehat{B_{2}}\) ( vì \(BI\) là phân giác góc B)

Suy ra \(∆BID=∆BIE\)  (cạnh huyền - góc nhọn)

Suy ra \(ID=IE\) (hai cạnh tương ứng)        (1)

Xét hai tam giác vuông \(CIF\) và \(CIE\) có:

+) \(CI\) cạnh chung

+) \(\widehat{C_{1}}=\widehat{C_{2}}\) ( vì \(CI\) là phân giác góc C)

Suy ra \(∆CIF=∆CIE\) (cạnh huyền - góc nhọn).

Suy ra: \(IE =IF\) (hai cạnh tương ứng)      (2)

Từ (1) và (2) suy ra: \(ID=IE=IF\).

loigiaihay.com

Bài 42 trang 124 - Sách giáo khoa toán 7 tập 1

Cho tam giác ABC có \(\widehat{A}\)= 90⁰, kẻ AH vuông góc với BC(H∈BC). C ác tam giác AHC và BAC  có AC là cạnh chung,   là góc chung,  \(\widehat{AHC}\)=\(\widehat{BAC}\)=90⁰,

nhưng hai tam giác không bằng nhau. Tại sao ở đây không áp dụng trường hợp góc cạnh góc để kết luận  

∆AHC= ∆BAC?

Giải:

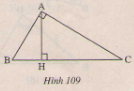
Các tam giác AHC và BAC có:

AC là cạnh chung 

\(\widehat{C}\) góc chung.

  \(\widehat{AHC}\)=\(\widehat{BAC}\)=90⁰,    

Nhưng hai tam giác  không bằng nhau vì góc AHC  không phải là góc kề với AC.

Bài 43 trang 125 - Sách giáo khoa toán 7 tập 1

Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA<OB.

Lấy các điểm C,D thuộc tia Oy sao cho OC=OA, OD=OB. Gọi E là giao điểm của AD và BC.

Chứng minh rằng:

a) AD=BC;

b) ∆EAB=∆ECD;

c )OE là tia phân giác của xOy.

 Giải:

a) ∆OAD và ∆OCB có: OA= OC(gt)

\(\widehat{AOD}\)=\(\widehat{COB}\)(=\(\widehat{A}\))

OD=OB(gt)

Nên ∆OAD=∆OCB(c.g.c)

suy ra AD=BC.

b) ∆OAD=∆OCB(cmt)

Suy ra: \(\widehat{D}\)= \(\widehat{B}\)

 \(\widehat{A_{1}}\)=\(\widehat{C _{1}}\) => \(\widehat{A _{2}}\)=\(\widehat{ C _{2}}\)

Do đó ∆AOE = ∆OCE(c .c.c)

suy ra: \(\widehat{ OAE}\)=\(\widehat{ COE}\)

vậy OE là tia phân giác của xOy.

b) ∆AEB= ∆CED(câu b) => EA=EC.

∆OAE và ∆OCE có: OA=OC(gt)

EA=EC(cmt)

OE là cạnh chung.

Nên ∆OAE=∆(OCE)(c .c.c)

suy ra: \(\widehat{ AOE}\)=\(\widehat{ C OE}\)

vậy OE là tia phân giác của góc xOy.

Bài 44 trang 125 - Sách giáo khoa toán 7 tập 1

Cho tam giác ABC có \(\widehat{ B}\)=\(\widehat{ C}\). Tia phân giác của góc A cắt BC tại D.

Chứng minh rằng.

a)  ∆ADB=∆ADC.

b) AB=AC.

Giải:

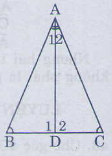
a) ∆ADB và ∆ ACD có:

 \(\widehat{ B}\)=\(\widehat{ C}\)(gt)                                      (1)

\(\widehat{ A_{1}}\)=\(\widehat{ A_{2}}\)(AD là tia phân giác)

Nên \(\widehat{ D_{1}}\)=\(\widehat{ D_{2}}\)

AD cạnh chung.

Do đó ∆ADB=∆ADC(g.c.g)

b) ∆ADB=∆ADC(câu a)

Suy ra AB=AC .

Bài 45 trang 125 - Sách giáo khoa toán 7 tập 1

Đố:  Cho 4 đoạn thẳng AB,BC,CD,DA trên giấy kẻ ô vuông như ở hinh 110. Hãy lập luận để giải thích:

a) AB=CD, BC=AD;

b) AB//CD.

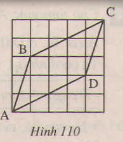
Giải: 

∆AHB và ∆ CKD có: 

HB=KD.

\(\widehat{ AHB}\)=\(\widehat{ CKD}\)

AH=Ck

Nên ∆ AHB = ∆  CKD(c.g.c)

suy ra AB=CD.

tương tự ∆ CEB = ∆ AFD(c.g.c)

suy ra BC=AD.

b) ∆ABD và ∆CDB  có:

AB=CD(câu a)

BC=AD(câu a)

BD chung.

Do đó ∆ABD=∆CDB(c.c .c)

Suy ra \(\widehat{ ABD}\)=\(\widehat{ CDB}\)

Vậy AB // CD( hai góc so le trong bằng nhau) 

Giaibaitap.me