Bài 29 trang 120 - Sách giáo khoa toán 7 tập 1
Cho góc \(xAy\). Lấy điểm \(B\) trên tia \(Ax\), điểm \(D\) trên tia \(Ay\) sao cho \(AB=AD\).Trên tia \(Bx\) lấy điểm \(E\), trên tia \(Dy\) lấy điểm \(C\) sao cho \(BE=DC\). Chứng minh rằng \(\Delta ABC = \Delta ADE\).
Giải:
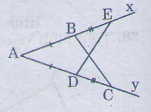
Ta có: \(AC=AD+DC\)
\(AE= AB+BE\)
Do \(AD=AB, DC=BE\)
Nên \(AC=AE\).
Xét \(∆ABC\) và \(∆ ADE\) có:
+) \(AC=AE\) (chứng minh trên)
+) \(\widehat{A}\) chung
+) \(AB=AD\) (gt)
Vậy \(∆ABC =∆ADE(c.g.c)\)
Bài 30 trang 120 - Sách giáo khoa toán 7 tập 1
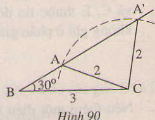
Trên hình 90, các tam giác ABC và A'BC có cạnh chung BC= 3cm cạnh chung BC = 3cm, CA=CA'= 2cm,\(\widehat{ABC }\)=\(\widehat{A'BC }\)= 300nhưng hai tam giác đó không bằng nhau.
Tại sao ở đây không áp dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C'?
Giải:
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được
Bài 31 trang 120 - Sách giáo khoa toán 7 tập 1
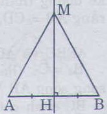
Cho độ dài đoạn thẳng AB, điểm nằm trên đường trung trực của AB, so sánh độ dài các đoạn MA,MB.
Giải:
Goi H là trung giao điểm của đường trung trực với đoạn AB,∆AHM=∆BHM(c .g.c )
Vậy MA= MB(hai cạnh tương ứng).
Bài 32 trang 120 - Sách giáo khoa toán 7 tập 1
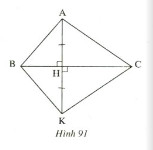
Bài 32. Tìm các tia phân giác trên hình 91. Hãy chứng minh điều đó.
Giải:
Xét \(∆AHB\) và \(∆KHB\) có
+) \(AH=KH\) (gt)
+) \(\widehat{AHB }=\widehat{KHB }\) (\(=90^0\))
+) \(BH\) cạnh chung .
Suy ra \(∆AHB=∆KHB\) (c.g.c)
suy ra: \(\widehat{ABH }=\widehat{KBH }\) (hai góc tương ứng)
Vậy \(BH\) là tia phân giác của góc \(B\).
Xét \(∆AHC\) và \(∆KHC\)
+) \(HC\) cạnh chung
+) \(\widehat{AHC }=\widehat{KHC }\) (\(=90^0\))
+) \(HA=HK\) (gt)
Suy ra \(∆AHC =∆KHC\) (c.g.c)
Suy ra: \(\widehat{ACH }=\widehat{KC H }\) (hai góc tương ứng).
Vậy \(CH\) là tia phân giác của góc \(C\)
Giaibaitap.me
Giải bài tập trang 123 bài 5 Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (g.c.g) Sách giáo khoa (SGK) Toán 7. Câu 33: Vẽ tam giác ABC biết AC...
Giải bài tập trang 123, 124 bài 5 Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (g.c.g) Sách giáo khoa (SGK) Toán 7. Câu 33: Trên mỗi hình 101,102,103 có tam giác nào bằng nhau...
Giải bài tập trang 124, 125 bài 5 Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (g.c.g) Sách giáo khoa (SGK) Toán 7. Câu 41:Cho tam giác ...
Giải bài tập trang 127 bài 6 Tam giác cân Sách giáo khoa (SGK) Toán 7. Câu 46: Dùng thước có chia xentimét và compa...
