Bài 1 trang 9 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

Thay ? bằng kí hiệu \( \in ,\, \notin \) thích hợp

Lời giải:

\(\begin{array}{l} - 7 \notin \mathbb{N};\,\,\,\,\,\,\, - 17 \in \mathbb{Z};\,\,\,\,\,\,\,\,\,\,\, - 38 \in Q\\\frac{4}{5} \notin \mathbb{Z};\,\,\,\,\,\,\,\,\,\,\,\frac{4}{5} \in \mathbb{Q};\,\,\,\,\,\,\,\,\,\,\,\,\,\,0,25 \notin \mathbb{Z};\,\,\,\,\,3,25 \in Q\end{array}\)

Bài 2 trang 9 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

a)      Trong các số sau, những phân số nào biểu diễn số hữu tỉ \(\frac{{ - 5}}{9}\)?

\(\frac{{ - 10}}{{18}};\,\frac{{10}}{{18}};\,\frac{{15}}{{ - 27}};\, - \frac{{20}}{{36}};\,\frac{{ - 25}}{{27}}.\)

b)      Tìm số đối của mỗi số sau: \(12;\,\frac{{ 4}}{9};\, - 0,375;\,\frac{0}{5};\,-2\frac{2}{5}.\)

Lời giải:

a) Ta có:

\(\begin{array}{l}\frac{{ - 10}}{{18}} =\frac{{ - 10:2}}{{18:2}} = \frac{{ - 5}}{9};\,\,\,\\\frac{{10}}{{18}} = \frac{{10:2}}{{18:2}} =\frac{5}{9};\,\,\\\,\frac{{15}}{{ - 27}} =\frac{{15:(-3)}}{{ - 27:(-3)}} = \frac{{ - 5}}{9};\,\\ - \frac{{20}}{{36}} =- \frac{{20:4}}{{36:4}}= \frac{{ - 5}}{9}.\end{array}\)

Vậy những phân số nào biểu diễn số hữu tỉ \(\frac{{ - 5}}{9}\) là: \(\frac{{ - 10}}{{18}};\,\frac{{15}}{{ - 27}};\, - \frac{{20}}{{36}}.\)

b) Số đối của các số \(12;\,\frac{{ 4}}{9};\, - 0,375;\,\frac{0}{5};\,-2\frac{2}{5}\) lần lượt là: \( - 12;\,\frac{-4}{9};\,0,375;\,\frac{0}{5};\, 2\frac{2}{5}\).

Bài 3 trang 9 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

a)      Các điểm A,B,C trong Hình 8 biểu diễn số hữu tỉ nào?

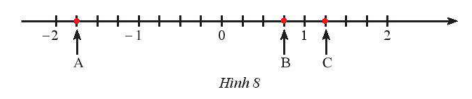
b)      Biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số.

Lời giải:

a)      Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: \(\frac{{ - 7}}{4};\,\frac{3}{4};\,\frac{5}{4}.\)

b)      Ta có: \(1\frac{1}{5} = \frac{6}{5};\,\,\, - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}.\)

Vậy ta biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số như sau:

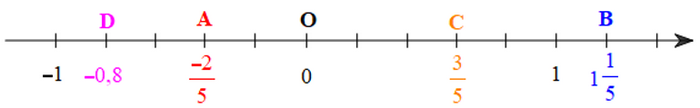
Bài 4 trang 10 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

a)      Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

\(\frac{5}{{12}};\, - \frac{4}{5};\,2\frac{2}{3};\, - 2;\,\frac{0}{{234}};\, - 0,32.\)

b)      Hãy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn.

Lời giải:

a) Các số hữu tỉ dương là: \(\frac{5}{{12}};\,2\frac{2}{3}.\)

Các số hữu tỉ âm là: \( - \frac{4}{5}; - 2;\, - 0,32.\)

Số không là số hữu tỉ dương cũng không là số hữu tỉ âm là: \(\frac{0}{{234}}\).

b) Ta có: \( - \frac{4}{5} = -0,8\)

Vì 0 < 0,32 < 0,8 < 2 nên 0 > -0,32 > -0,8 > -2 hay \(-2 < - \frac{4}{5} < -0,32 < 0\)

Mà \(0 < \frac{5}{12} <1; 1<2\frac{2}{3}\) nên \(0 < \frac{5}{12} < 2\frac{2}{3}\)

Các số theo thứ tự từ nhỏ đến lớn là:

\(-2 ; - \frac{4}{5} ; -0,32; \frac{0}{{234}}; \frac{5}{12} ; 2\frac{2}{3}\)

Chú ý: \(\frac{0}{a} = 0\,,\,a \ne 0.\)

Bài 5 trang 10 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

So sánh các cặp số hữu tỉ sau:

a)      \(\frac{2}{{ - 5}}\) và \(\frac{{ - 3}}{8}\)                b) \( - 0,85\) và \(\frac{{ - 17}}{{20}}\);

c) \(\frac{{ - 137}}{{200}}\)  và \(\frac{{37}}{{ - 25}}\)         d) \( - 1\frac{3}{{10}}\) và \(-\left( {\frac{{ - 13}}{{ - 10}}} \right)\).

Lời giải:

a)      Ta có: \(\frac{2}{{ - 5}} = \frac{{ - 16}}{{40}}\) và \(\frac{{ - 3}}{8} = \frac{{ - 15}}{{40}}\)

Do \(\frac{{ - 16}}{{40}} < \frac{{ - 15}}{{40}}\,\, \Rightarrow \,\frac{2}{{ - 5}} < \frac{{ - 3}}{8}\).

b)      Ta có: \( - 0,85 = \frac{{ - 85}}{{100}} = \frac{{ - 17}}{{20}}\). Vậy \( - 0,85\)=\(\frac{{ - 17}}{{20}}\).

c)      Ta có: \(\frac{{37}}{{ - 25}} = \frac{{ - 296}}{{200}}\)  

Do  \(\frac{{ - 137}}{{200}} > \frac{{ - 296}}{{200}}\) nên \(\frac{{ - 137}}{{200}}\) > \(\frac{{37}}{{ - 25}}\) .

d)      Ta có: \( - 1\frac{3}{{10}}=\frac{-13}{10}\) ;

\(-\left( {\frac{{ - 13}}{{ - 10}}} \right) = \frac{{-13}}{{10}}\).

Vậy \(- 1\frac{3}{{10}} =-(\frac{{-13}}{{-10}})\,\).

Bài 6 trang 10 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

So sánh các cặp số hữu tỉ sau:

a) \(\frac{{ - 2}}{3}\) và \(\frac{1}{{200}}\);          b) \(\frac{{139}}{{138}}\) và \(\frac{{1375}}{{1376}}\);      c) \(\frac{{ - 11}}{{33}}\) và \(\frac{{25}}{{ - 76}}\).

Lời giải:

a)      Ta có \(\frac{{ - 2}}{3} < 0\) và \(\frac{1}{{200}} > 0\) nên \(\frac{{ - 2}}{3}\)<\(\frac{1}{{200}}\).

b)      Ta có: \(\frac{{139}}{{138}} > 1\) và \(\frac{{1375}}{{1376}} < 1\) nên \(\frac{{139}}{{138}}\) > \(\frac{{1375}}{{1376}}\).

c)      Ta có: \(\frac{{ - 11}}{{33}} = \frac{{ - 1}}{3}\) và \(\frac{{25}}{{ - 76}} = \frac{{ - 25}}{{76}} > \frac{{ - 25}}{{75}} = \frac{{ - 1}}{3}\,\,\,\, \Rightarrow \frac{{25}}{{ - 76}} > \frac{{ - 11}}{33}\).

Bài 7 trang 10 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

Bảng dưới đây cho biết độ cao của bốn rãnh đại dương so với mực nước biển.

(Theo: https://vi.wikipedia.org/wiki/Rãnh_đại_dương)

a) Những rãnh đại dương nào có độ cao cao hơn rãnh Puerto Rico? Giải thích.

b) Rãnh đại dương nào có độ cao thấp nhất trong bốn rãnh trên? Giải thích.

Lời giải:

Ta có: \( - 10,5 <  - 8,6 <  - 8,0 <  - 7,7\).

Vậy ta có thứ tự các độ cao từ thấp đến cao là: Rãnh Philippine, rãnh Puerto Rico, rãnh Peru-Chile, rãnh Romanche.

a)      Những rãnh có độ cao cao hơn rãnh Puerto Rico là: rãnh Peru-Chile, rãnh Romanche vì -7,7 > -8,0 > -8,6

b)      Rãnh đại dương nào có độ cao thấp nhất trong bốn rãnh trên là: rãnh Philippine vì - 10,5 <  - 8,6 <  - 8,0 <  - 7,7

Giaibaitap.me